Cho tam giác ABC vuông tại A có AB = 15, AC = 20. a) Tính tỉ số lượng giác của B.
Câu hỏi:
Cho tam giác ABC vuông tại A có AB = 15, AC = 20.
a) Tính tỉ số lượng giác của B.
b) Vẽ đường cao AH. Tính độ dài các đoạn AH, HB, HC.
c) Gọi D và E lần lượt là trung điểm của BH và AH .Tia CE cắt AD tại M. Chứng minh CM =AM. cos.
Trả lời:
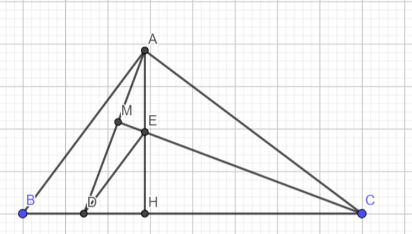
a) Ta có ΔABC vuông tại A
⇒ BC2 = AB2 + AC2 = 625
⇒ BC = 25
⇒ sinB
b) Ta có AH ⊥ BC
⇒ AH.BC = AB.AC(= 2SABC)
⇒ AH =
⇒ HB = HC = BC – HB = 25 – 9 = 16
c) Ta có D, E là trung điểm HB, HA
⇒ DE là đường trung bình ΔHAB
⇒ DE // AB
⇒ DE ⊥ AC vì AB⊥AC
Mà AH ⊥ BC ⇒AH ⊥ CD, AH ∩ DE = E
⇒ E là trực tâm ΔADC ⇒ CE ⊥ AD
⇒ CM ⊥ AD
⇒
⇒ cos =
⇒ CM = AC.cos