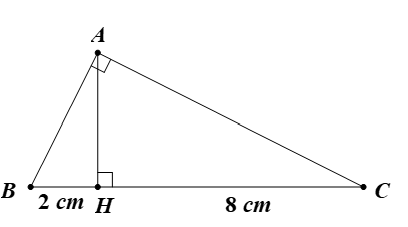
Cho tam giác ABC vuông tại A có đường cao AH chia cạnh huyền BC thành BH = 2 cm, CH = 8 cm. Giải tam giác vuông này.
Câu hỏi:
Cho tam giác ABC vuông tại A có đường cao AH chia cạnh huyền BC thành BH = 2 cm, CH = 8 cm. Giải tam giác vuông này.
Trả lời:
Ta có: BC = BH + CH = 2 + 8 = 10 (cm).
Áp dụng hệ thức lượng cho tam giác ABC vuông tại A có AH là đường cao, ta được:
⦁ AB2 = BH.BC = 2.10 = 20. Suy ra (cm).
⦁ AC2 = CH.BC = 8.10 = 80. Suy ra (cm).
Tam giác ABC vuông tại A:
⦁ . Suy ra .
⦁ .
Vậy BC = 10 cm; cm; cm; và .
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Một mảnh đất hình chữ nhật có chu vi 96 m, chiều dài bằng chiều rộng. Người ta đã sử dụng diện tích mảnh đất để xây nhà. Tính diện tích phần đất xây nhà.
Xem lời giải »
Câu 2:
Một sân vườn hình chữ nhật có chu vi là 64 m, chiều dài gấp 3 lần chiều rộng.
a) Tính diện tích khu vườn.
Xem lời giải »
Câu 3:
b) Người ta dự định rào khu vườn bằng lưới kẽm. Biết mỗi mét lưới kẽm giá 100 000 đồng. Tính số tiền mua lưới.
Xem lời giải »
Câu 4:
Một vườn hoa có diện tích 800 m2 nằm trong công viên có diện tích 25 ha. Hỏi diện tích vườn hoa chiếm bao nhiêu phần diện tích công viên?
Xem lời giải »
Câu 5:
Cho IX = V – I. Hãy đổi chỗ 2 que tính để được phép tính mới bằng 1, rồi viết phép tính đó bằng số La Mã.
Xem lời giải »
Câu 6:
Khi lấy tổng các số tự nhiên từ 1 đến 49 cộng với 25 ta được kết quả là
Xem lời giải »