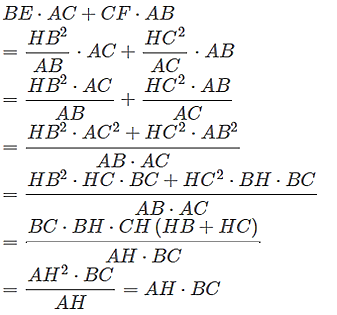Cho tam giác ABC vuông tại A đường cao AH. E, F lần lượt là hình chiếu của H lên AB, AC. Chứng minh: BE . AC + CF . AB = AH . BC.
Câu hỏi:
Cho tam giác ABC vuông tại A đường cao AH. E, F lần lượt là hình chiếu của H lên AB, AC. Chứng minh: BE . AC + CF . AB = AH . BC.
Trả lời:
Lời giải
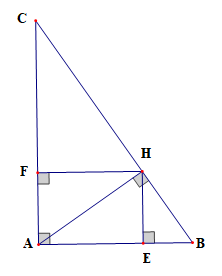
Xét tam giác ABH vuông ở H có HE ⊥ AB, theo hệ thức lượng trong tam giác vuông ta có HB2 = BE . AB
Suy ra \(BE = \frac{{H{B^2}}}{{AB}}\)
Xét tam giác ACH vuông ở H có HF ⊥ AC, heo hệ thức lượng trong tam giác vuông ta có
HC2 = CF . AC
Suy ra \(CF = \frac{{H{C^2}}}{{AC}}\)
Xét tam giác ACB vuông ở A có AH ⊥ BC
Theo hệ thức lượng trong tam giác vuông ta có
AC2 = CH . BC
AB2 = BH . BC
Suy ra
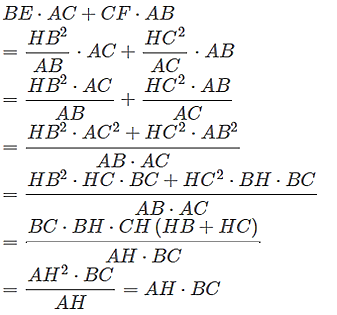
Vậy BE . AC + CF . AB = AH . BC.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Nhân ngày 20 tháng 10 một cửa hàng thời trang giảm 30% giá niêm yết cho tất cả sản phẩm. Đặc biệt nếu khách hàng nào có thẻ khách hàng thân thiện của cửa hàng thì được tặng thêm một voucher trị giá bằng 10% số tiền thanh toán tại quầy Thu Ngân:
a) Chị Hoa không có thẻ khách hàng thân thiện của cửa hàng, chị mua một chiếc váy có giá niêm yết là 1 050 000 đồng. Hỏi chị Hoa phải trả bao nhiêu tiền cho chiếc váy đó?
b) Cô Hà có thẻ khách hàng thân thiện, cô mua 1 chiếc túi xách và nhận được một voucher trị giá 91 000 đồng. Hỏi giá niêm yết ban đầu của túi xách là bao nhiêu?
Xem lời giải »
Câu 2:
Tam giác ABC có BC = 21 cm, CA = 17 cm, AB = 10 cm. Tính bán kính R của đường tròn ngoại tiếp tam giác ABC
Xem lời giải »
Câu 3:
Tìm tất cả các số nguyên x, y, z thỏa mãn 3x2 + 6y2 + 2z2 + 3y2z2 – 18x = 6.
Xem lời giải »
Câu 4:
Cho tam giác ABC vuông tại A, đường cao AH. Gọi E, F lần lượt là hình chiếu H trên AB, AC. Chứng minh:
a) \(\frac{{FB}}{{FC}} = \frac{{A{B^3}}}{{A{C^3}}}\);
b) BC2 = 3AH2 + BE2 + CF2;
c) \(BE\sqrt {CH} + CF\sqrt {BH} = AH\sqrt {BC} \).
Xem lời giải »
Câu 5:
Cho tam giác ABC vuông tại A và đường cao AH. Biết \(\widehat A = 90^\circ \), AB = 15 cm, AC = 20 cm.
a) Tính cạnh BC.
b) Tính độ dài của AH, BH và HC.
Xem lời giải »
Câu 6:
Cho tứ giác ABCD nội tiếp (O). Gọi E là giao điểm của AB, CD. F là giao điểm của AC và BD. Đường tròn ngoại tiếp tam giác BDE cắt đường tròn ngoại tiếp tam giác FDC tại điểm K khác D. Tiếp tuyến của (O) tại B và C cắt nhau tại M.
a) Chứng minh tứ giác BKCM nội tiếp.
b) Chứng minh E, M, F thẳng hàng.
Xem lời giải »
Câu 7:
Cho đoạn thẳng AB. Gọi O là trung điểm của AB. Vẽ về 1 phía AB các tia Ax và By vuông góc với AB. Lấy C trên Ax, D trên By sao cho \(\widehat {CO{\rm{D}}} = 90^\circ \)
a) Chứng minh rằng:
b) Chứng minh rằng: CD = AC + BD
c) Kẻ OM ⊥ CD tại M, gọi N là giao điểm của AD với BC. Chứng minh rằng MN // AC.
Xem lời giải »
Câu 8:
Cho đoạn thẳng AB. Trên cùng một nửa mặt phẳng bờ AB kẻ hai tia Ax, By vuông góc với AB. Trên tia Ax và By lần lượt lấy hai điểm C và D sao cho \(\widehat {CO{\rm{D}}} = 90^\circ \) (O là trung điểm của AB). Chứng minh rằng:
a) CD = AC + BD
b) CD là tiếp tuyến của đường tròn đường kính AB
c) \(AC.B{\rm{D}} = \frac{{A{B^2}}}{4}\).
Xem lời giải »