Cho tứ diện ABCD có AB = AC = BC = 2; AD = 4; góc BAD = góc CAD = 60 độ. Tính
Câu hỏi:
Cho tứ diện ABCD có AB = AC = BC = 2; AD = 4; \(\widehat {BAD} = \widehat {CAD} = 60^\circ \). Tính thể tích khối tứ diện ABCD?
Trả lời:
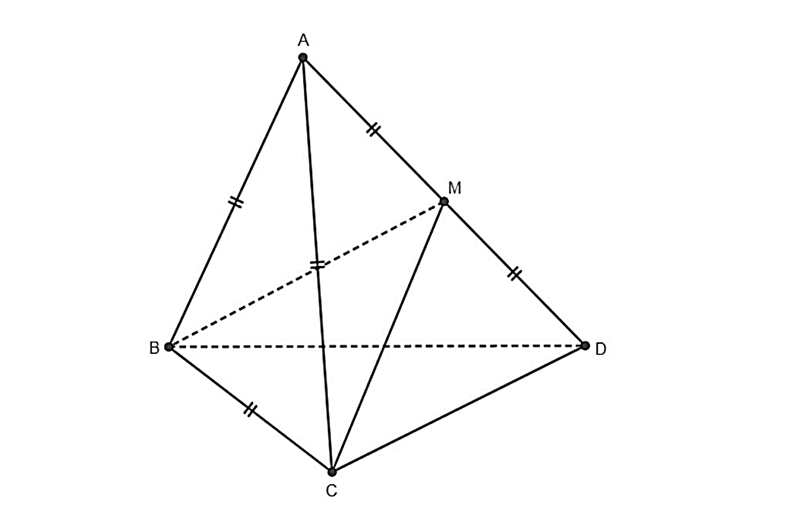
Ta có AB = AC = BC = 2 nên tam giác ABC đều
Suy ra: \(\widehat {BAC} = 60^\circ \)
Gọi M là trung điểm AD
Suy ra: \(\left\{ \begin{array}{l}AM = \frac{1}{2}AD = 2\\\widehat {BAM} = \widehat {CAM} = 60^\circ \end{array} \right.\)
Xét tứ diện ABCM có:
\(\left\{ \begin{array}{l}AB = AC = AM = 2\\\widehat {BAM} = \widehat {CAM} = 60^\circ \end{array} \right.\)
Suy ra: ABCM là tứ điện đều
VABCM = \(\frac{{A{B^3}\sqrt 2 }}{{12}} = \frac{{2\sqrt 2 }}{3}\)
Áp dụng công thức tỉ số thể tích khối chóp tam giác, ta được:
\(\frac{{{V_{ABCM}}}}{{{V_{ABCD}}}} = \frac{{AM}}{{AD}} = \frac{1}{2}\)
Suy ra: VABCD = 2VABCM = \(\frac{{4\sqrt 2 }}{3}\).

