Hình thang ABCD (AB//CD) có DC = 2AB. Gọi M, N, P, Q lần lượt là trung điểm của các
Câu hỏi:
Hình thang ABCD (AB//CD) có DC = 2AB. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA.
a) Chứng minh các tứ giác ABPD, MNPQ là hình bình hành.
b) Tìm điều kiện của hình thang ABCD để MNPQ là hình thoi.
c) Gọi E là giao điểm của BD và AP. Chứng minh Q, N, E thẳng hàng.
Trả lời:
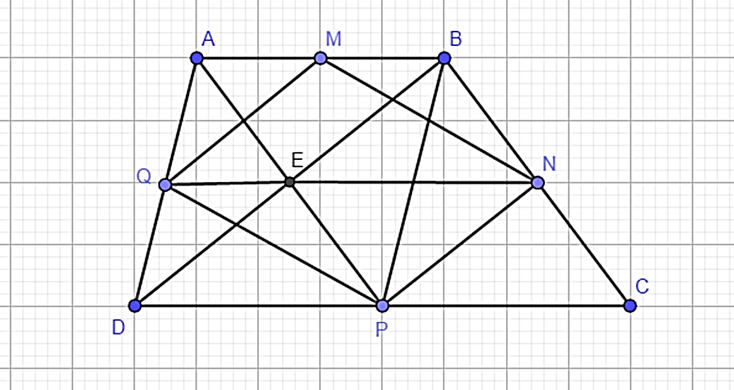
a) Do DC = 2AB mà P là trung điểm DC nên AB = DP = PC
Tứ giác ABPD có AB // DP và AB = DP nên ABPD là hình bình hành
M, N, P, Q thứ tự là trung điểm các cạnh AB, BC, CD, DA nên ta có:
MQ là đường trung bình trong tam giác ABD nên MQ // BD và MQ = \(\frac{1}{2}\)BD
NP là đường trung bình trong tam giác CBD nên NP // BD và NP = \(\frac{1}{2}\)BD
Suy ra tứ giác MNPQ có NP // MQ và NP = MQ nên MNPQ là hình bình hành.
b) Để MNPQ là hình thoi thì MQ = MN ⇔ \(\frac{1}{2}\)BD = \(\frac{1}{2}\)AC ⇔ AC = BD
Suy ra ABCD là hình thang cân thì MNPQ là hình thoi
c) ABPD là hình bình hành nên E là giao điểm của BD và AP thì E là trung điểm của BD
QE là đường trung bình trong tam giác DAB nên QE // AB
EN là đường trung bình trong tam giác BCD nên EN // DC
Mà AB // DC nên Q, E, N thẳng hàng.

