Một công ty cần thuê xe vận chuyển 140 người và 9 tấn hàng hóa. Nơi cho thuê xe chỉ có 10 xe hiệu M và 9 xe hiệu F. Một chiếc xe hiệu M có thể chở 20 người và 0,6 tấn hàng. Một chiếc xe hiệu
Câu hỏi:
Một công ty cần thuê xe vận chuyển 140 người và 9 tấn hàng hóa. Nơi cho thuê xe chỉ có 10 xe hiệu M và 9 xe hiệu F. Một chiếc xe hiệu M có thể chở 20 người và 0,6 tấn hàng. Một chiếc xe hiệu F có thể chở 10 người và 1,5 tấn hàng. Tiền thuê một xe hiệu M là 4 triệu đồng, một xe hiệu F là 3 triệu đồng. Hỏi nếu thuê xe mỗi loại lần lượt là bao nhiêu để chi phí thấp nhất?
Trả lời:
Gọi x; y lần lượt là số xe loại M, loại F cần thuê
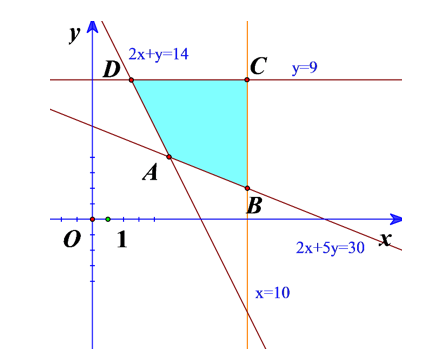
Từ bài toán ta được hệ bất phương trình:
Tổng chi phí T (x; y) = 4x + 3y (triệu đồng)
Bài toán trở thành là tìm x; y nguyên không âm thoả mãn hệ (*) sao cho T (x; y) nhỏ nhất.
Khi đó T (x; y) = 4x + 3y sẽ đạt giá trị nhỏ nhất trên miền nghiệm của hệ bất phương trình (*) khi (x; y) là tọa độ của một trong các đỉnh:
Ta tính được
Suy ra T (x; y) nhỏ nhất khi (x; y) = (5; 4).
Từ đó ta cần thuê 5 xe hiệu M và 4 xe hiệu F thì chi phí vận tải là thấp nhất.