Người ta dự định dùng hai loại nguyên liệu để chiết xuất ít nhất 140kg chất A và 9kg

Gọi x là số tấn nguyên liệu loại I, y là số tấn nguyên liệu loại II cần dùng.

Số tiền để mua nguyên liệu là 4x + 3y (triệu đồng)

Theo bài ra ta có hệ bất phương trình: $\left\{\begin{array}{l}0\le x\le 10\\ 0\le y\le 9\\ 2x+y\ge 14\\ 2x+5y\ge 30\end{array}\right.$ (1)

Yêu cầu bài toán trở thành: Tìm (x; y) thỏa mãn (1) để F(x; y) = 4x + 3y đạt giá trị nhỏ nhất

Vẽ và xác định miền nghiệm của (1)

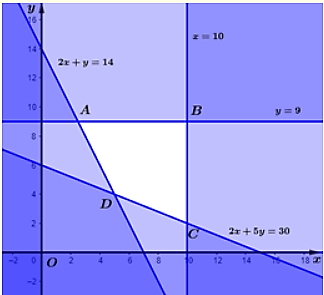
Miền nghiệm của (1) là tứ giác ABCD (kể cả biên)

$A\left(\frac{5}{2};9\right),B\left(10;9\right),C\left(10;2\right),D\left(5;4\right)$

F(x; y) = 4x + 3y

F(A) = 37; F(B) = 67; F(C) = 32; F(D) = 32

Suy ra: min F(x; y) = F(D) = 32 khi x = 5; y = 4

Vậy để chi phí mua nguyên liệu là ít nhất thì cần mua 5 tấn nguyên liệu loại I và 4 tấn nguyên liệu loại II.