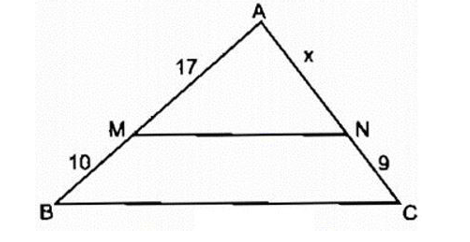
Tìm n để 5n − 2n chia hết cho 63.
Câu hỏi:
Trả lời:
+) TH1:
Để 5n ⁝ 63 thì 5n = 63.k mà 5n ⁝ 5 tuy vậy nên 5n không thể chia hết cho 63.
Vậy TH1 không thể xảy ra.
+) TH2: 5n chia cho 63 dư 1, 2n chia cho 63 dư 1.
- Xét n = 0 thì 5n = 1 và 2n = 1
Suy ra 5n − 2n = 1 − 1 = 0 ⁝ 63
- Xét n > 0 ta có:
Ta thử được 56 = 15625 chia cho 63 dư 1
26 = 64 chia cho 63 dư 1
Nên đặt n = 6k (k Î ℕ*) thì:
56k − 26k = (56)k − (26)k = (15625)k − (64)k
≡ 1k − 1k ≡ 0 (mod 63)
Vậy với n = 6k (k Î ℕ) thì: 5n − 2n chia hết cho 63.