Trên cùng phía của đường thẳng xy, vẽ 2 đường thằng AH và BK, sao cho AH vuông
Câu hỏi:
Trên cùng phía của đường thẳng xy, vẽ 2 đường thằng AH và BK, sao cho AH vuông góc với xy ở H, BK vuông góc với xy ở K và BK = AH. Gọi O là trung điểm của đoạn HK. Chứng minh: \(\widehat {AOH} = \widehat {BOK}\).
Trả lời:
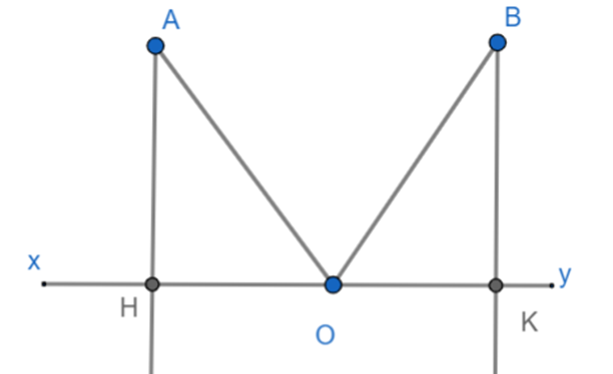
Ta có: AH ⊥ xy ⇒ \[\widehat {AHO} = 90^\circ \]
BK ⊥ xy ⇒ \[\widehat {BKO} = 90^\circ \]
Xét △AHO vuông tại H và △BKO vuông tại K có:
AH = BK
\[\widehat {AHO} = \widehat {BKO} = 90^\circ \]
HO = OK (do O là trung điểm của HK)
⇒ △AHO = △BKO (c.g.c)
⇒ \(\widehat {AOH} = \widehat {BOK}\)(2 góc tương ứng).

