Cho điểm M nằm ngoài đường tròn ( O; R ) sao cho OM = 2R. Từ M
Câu hỏi:
Cho điểm M nằm ngoài đường tròn ( O; R ) sao cho OM = 2R. Từ M kẻ các tiếp tuyến MA, MB với đường tròn O (A, B là các tiếp điểm ). Kẻ đường kính AC của đường tròn (O). Gọi H là giao điểm của AB và OM.
a) Chứng minh 4 điểm : O, A, B, M cùng thuộc 1 đường tròn.
b) Tính tỉ số OHOM .
c) Gọi E là giao điểm của CM và đường tròn (O). Chứng minh HE vuông góc với BE.
Trả lời:
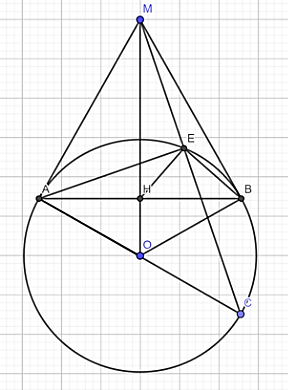
a) Vì MA, MB là tiếp tuyến của (O)
⇒ MA ⊥ OA ⇒ ^MAO = 90°
⇒ MB ⊥ OB ⇒ ^MBO = 90°
^MAO+^MBO= 90° + 90° = 180°
⇒ OAMB là tứ giác nội tiếp
⇒ O, A, B, M cùng thuộc 1 đường tròn (đpcm)
b) Vì MA, MB là tiếp tuyến của (O) kẻ từ M
⇒ M cách đều A, B mà O cách đều A, B
⇒ MO là trung trực của AB
⇒ MO ⊥ AB tại H , H là trung điểm AB
Tam giác OAM vuông tại A có đường cao AH
Suy ra: OA2 = OH.OM
⇒ OH = R22R=R2
⇒ OHOM=R22R=14
c) Áp dụng hệ thức lượng trong tam giác MAO vuông có: MA2 = MH.MO (1)
MA là tiếp tuyến nên: ^MAE=^MCA (cùng chắn cung AE)
Xét ∆MAE và ∆MCA có: ^MAE=^MCA
^AMC chung
Suy ra: ∆MAE ~ ∆MCA (g.g)
⇒ MAME=MCMA hay MA2 = MC.ME (2)
Từ (1) và (2): MC.ME = MH.MO
⇒ MHME=MCMO
Xét ∆MHE và ∆MCO có:
^OMC chung
MHME=MCMO
⇒ ∆MHE ~ ∆MCO (c.g.c)
⇒ ^MHE=^MOC
⇒ 180° – ^MHE = 180° – ^MOC hay ^HEC=^AOM
Lại có: BEAC là tứ giác nội tiếp (O) do 4 điểm đều nằm trên đường tròn nên ^BEC=^BAC (cùng nhìn cạnh BC)
Lại có theo phần a: OBMA là tứ giác nội tiếp nên ^OMB=^BAO ; ^ABO=^OMA
Suy ra: ^BEC=^OMB
Lại có: ^ABO=^OMB (Cùng phụ với ^MBA )
Mà ^ABO=^OMA
Suy ra: ^BEC=^OMA
^HEB=^HEC+^BEC=^AOM+^OMA
= 90°
Vậy HE vuông góc với BE.
