Cho điểm M nằm ngoài đường tròn (O;R). Từ M kẻ các tiếp tuyến MA, MB tới đường
Câu hỏi:
Cho điểm M nằm ngoài đường tròn (O;R). Từ M kẻ các tiếp tuyến MA, MB tới đường tròn tâm O (A, B là các tiếp điểm). Gọi H là giao điểm của MO với AB. Kẻ đường kính AD của đường tròn (O), MD cắt đường tròn (O) tại điểm thứ hai là C. Chứng minh rằng \(\widehat {MHC} = \widehat {ADC}\).
Trả lời:
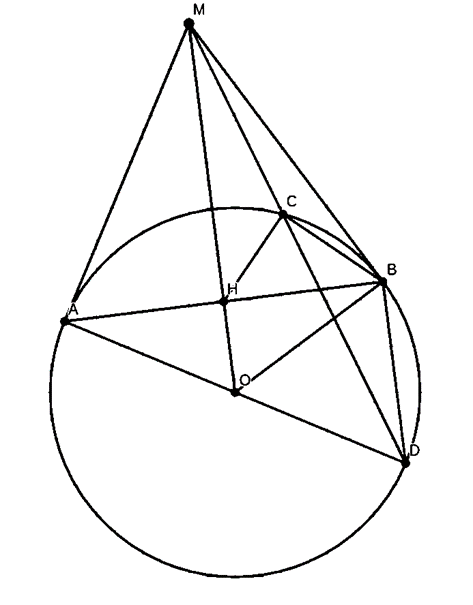
ΔOAM vuông tại A có AH⊥OM
⇒ AM2 = MH.MO (1)
Ta có: \(\widehat {ACD}\)= 90° (do AD là đường kính) ⇒ AC ⊥ DM
\(\widehat {OAM}\)=90° hay \(\widehat {DAM}\)= 90°
⇒ ΔADM vuông tại A có AC⊥DM
⇒AM2 = MC.MD (2)
Từ (1), (2)
⇒ MH.MO = MC.MD( =AM2)
⇒ \(\frac{{MH}}{{MD}} = \frac{{MC}}{{MO}}\)
Xét ΔMHC và ΔMDO có:
\(\widehat {OMD}\) chung
\(\frac{{MH}}{{MD}} = \frac{{MC}}{{MO}}\) (cmt)
⇒ ΔMHC ∽ ΔMDO(c−g−c)
⇒ \(\widehat {MHC} = \widehat {ADC}\).