Cho đường tròn (O), đường kính BC = 2R, điểm A nằm ngoài đường tròn sao cho tam
Câu hỏi:
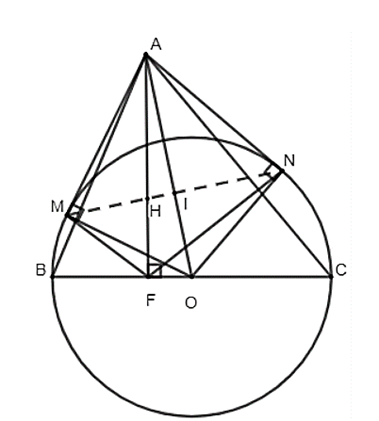
Cho đường tròn (O), đường kính BC = 2R, điểm A nằm ngoài đường tròn sao cho tam giác ABC nhọn. Từ A kẻ 2 tiếp tuyến AM, AN với đường tròn (O). Gọi H là trực tâm của tam giác ABC, F là giao điểm của AH và BC. Chứng minh rằng:
a) 5 điểm A, O, M, N, F cùng nằm trên 1 đường tròn.
b) 3 điểm M, N, H thẳng hàng.
c) HA . HF = R2 – OH2.
Trả lời:
a) \(\widehat {AMO} = \widehat {AFO} = \widehat {ANO} = 90^\circ \)
⇒ A, M, F, N, O cùng thuộc một đường tròn
b) Gọi I là giao của MN và AO nên I là trung điểm của MN ⇒ AI.AO = AM2
Xét ∆AMH và ∆AFM có:
\(\widehat {MAH}\)chung
\(\widehat {AMH} = \widehat {AFM}\)
Nên ∆AMH ~ ∆AFM (g.g)
⇒ AH.AF = AM2 = AI.AO
⇒ \(\widehat {AHI} = \widehat {AOF}\)
⇒ OFHI nội tiếp
⇒ M, N, H thẳng hàng
c) Từ câu a) ta có: HM.HN = HA.HF
Ta có: HM.HN = (IM – IH).(IH + IN)
= (IM – IH).(IH + IM)
= IM2 – IH2
= OM2 – OI2 – (OH2 – OI2)
= R2 – OH2
Từ đó suy ra: HA.HF = R2 – OH2.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho hình bình hành ABCD. Chứng minh rằng \(\overrightarrow {AB} + 2\overrightarrow {AC} + \overrightarrow {AD} = 3\overrightarrow {AC} \).
Xem lời giải »
Câu 2:
Cho biểu thức \(A = 1 + \left( {\frac{{2a + \sqrt a - 1}}{{1 - a}} - \frac{{2a\sqrt a - \sqrt a + a}}{{1 - a\sqrt a }}} \right).\frac{{a - \sqrt a }}{{2\sqrt a - 1}}\). Rút gọn A.
Xem lời giải »
Câu 4:
Rút gọn phân thức: \(\frac{{\left( {{x^2} + 3x + 2} \right)\left( {{x^2} - 25} \right)}}{{{x^2} + 7x + 10}}\).
Xem lời giải »
Câu 5:
Có 5 người trên 7 toa tàu được đánh số 1, 2, 3, 4, 5, 6, 7. Tính xác suất để 5 người lên 5 toa tàu khác nhau?
Xem lời giải »
Câu 6:
Giải phương trình: \(\sqrt 3 \cos \left( {x + \frac{\pi }{2}} \right) + \sin \left( {x - \frac{\pi }{2}} \right) = 2\sin 2x\).
Xem lời giải »
Câu 7:
Tính giá trị biểu thức M = cos215° + cos225° + cos235° + cos245° + cos2105° + cos2115° + cos2125°.
Xem lời giải »
Câu 8:
Một ca nô chạy trong hồ nước yên lặng có vận tốc tối đa 18 km/h. Nếu ca nô chạy ngang một con sông có dòng chảy theo hướng Bắc – Nam với vận tốc lên tới 5 m/s thì vận tốc tối đa nó có thể đạt được so với bờ sông là bao nhiêu và theo hướng nào?
Xem lời giải »


