Cho đường tròn (O,R) cố định. Từ M nằm ngoài đường tròn (O) kẻ 2 tiếp tuyến MA,MB (A,B là các tiếp điểm)

Cho đường tròn (O,R) cố định. Từ M nằm ngoài đường tròn (O) kẻ 2 tiếp tuyến MA,MB (A,B là các tiếp điểm). Gọi H là giao điểm của OM, AB.

a) Chứng minh: OM vuông góc với AB và OH.OM = R².

b) Từ M kẻ cát tuyến MNP với đường tròn (O) (N nằm giữa M,P), gọi I là trung điểm NP (I khác O). Chứng minh: A, M, O, I thuộc một đường tròn và tìm tâm của đường tròn đó.

c) Qua N kẻ tiếp tuyến với đường tròn (O), cắt MA, MB theo thứ tự C,D. Biết MA = 5cm, tính chu vi tam giác MCD.

d) Qua O kẻ đường thẳng d vuông góc với OM, cắt MA, MB lần lượt tại E, F. Xác định vị trí của điểm M để diện tích tam giác MEF nhỏ nhất.

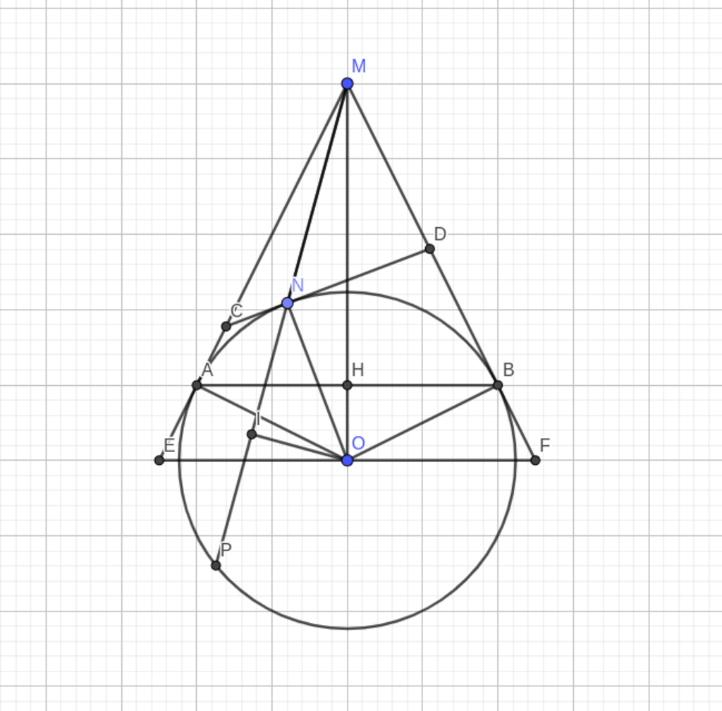
a) Ta có: MA, MB là tiếp tuyến của (O)

Suy ra: MO ⊥ AB tại H.

Ta có: MA ⊥ AO, AH ⊥ MO

⇒ OH.OM = OA² = R²

b) Do I là trung điểm NP ⇒ OI ⊥ NP

Mà MA ⊥ OA, MB ⊥ OB

⇒ M, A, I, O, B ∈ đường tròn đường kính OM

⇒ Tâm của đường tròn là trung điểm MO

c) Ta có : CN, CA là tiếp tuyến của (O) ⇒ CN = CA

Tương tự:

DN = DB

⇒ PMCD = MC + CD + DM = MC + CN + ND + DM

= MC + AC + DB + DM = MA + MB = 2MA = 10.

d) Ta có :

S_MEF = $\frac{1}{2}.MO.EF$

Mà OA ⊥ ME, MO ⊥ OE

⇒ $\frac{1}{O{A}^2}=\frac{1}{O{M}^2}+\frac{1}{O{E}^2}\ge \frac{2}{OM.OE}$

⇒ OM.OE ≥ 2OA² = 2R²

⇒ S_MEF ≥ $\frac{1}{2}.2R^2$= R²

Dấu = xảy ra khi OE = OM ⇒ ΔOEM vuông cân tại O

⇒ $\widehat{OMA}=45°$ ⇒ ΔAMO vuông cân tại A 

⇒ MO = OA$\sqrt{2}$ =  $R\sqrt{2}$