Cho đường tròn (O;R) và điểm A cố định ngoài đường tròn. Vẽ đường thẳng d vuông

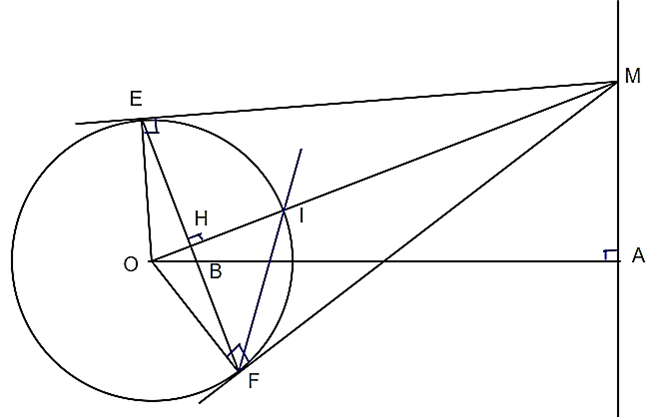
a) Do ME, MF là tiếp tuyến với đường tròn suy ra EF ⊥ OM

Tứ giác ABHM có \(\widehat A = \widehat H = 90^\circ \) nên tứ giác này nội tiếp đường tròn bán kính MB.

b) Xét ΔOHB và ΔOAM có:

Chung \(\widehat O\)

\(\widehat {OHB} = \widehat {OAM} = 90^\circ \)

⇒ ΔOHB ∽ ΔOAM (g.g)

⇒ \(\frac{{OH}}{{OA}} = \frac{{OB}}{{AM}}\)

⇒ OA.OB = OH.OM(1)

Tương tự: ΔOHE ∽ ΔOEM (g.g)

⇒ \(\frac{{OH}}{{OE}} = \frac{{OE}}{{OM}}\)

⇒ OH.OM = OE² = R²

⇒ OH.OM = R² (2)

Từ (1) và (2) suy ra: OA.OB = OH.OM = R²

c) Gọi I là giao điểm của OM với đường tròn (O). Nối FI.

Do  suy ra \(\widehat {MFI} = \widehat {EFI}\)

Suy ra FI là phân giác của góc \(\widehat {MFE}\)

Lại có MI là phân giác của góc \(\widehat {EMF}\)

Do đó I là giao điểm của đường phân giác trong của tam giác MEF

⇒ I là tâm đường tròn nội tiếp tam giác MEF.

Mà I thuộc đường tròn (O) cố định. Suy ra đpcm.

d) Diện tích tam giác HBO: S_HBO = \(\frac{1}{2}HO.HB\)

Xét ΔOHB ∽ ΔOAM (g.g)

⇒ \(\frac{{HB}}{{AM}} = \frac{{OB}}{{OM}}\)

⇒ HB.OM = AM.OB (3)

Có: OH.OM = R²(4)

Nhân (3) và (4) vế với vế ta được: OH.HB.OM² = R².AM.OB = R² . AM . \(\frac{{{R^2}}}{{OA}}\)

⇒ OH.HB = \({R^4}.\frac{{AM}}{{OA.O{M^2}}} = {R^4}.\frac{{AM}}{{OA.\left( {O{A^2} + A{M^2}} \right)}}\)

Áp dụng BĐT Cô si với OA và AM ta có: \(O{A^2} + A{M^2} \ge 2\sqrt {O{A^2}.A{M^2}} = 2.OA.AM\)

Dấu "=" xảy ra khi: OA = AM

⇒ OH.HB ≤ \({R^2}.\frac{{AM}}{{OA.2.OA.AM}} = \frac{{{R^2}}}{{4.O{A^2}}}\)

Suy ra: S_max = \(\frac{{{R^2}}}{{4.O{A^2}}}\) khi OA = AM.