Cho đường tròn (O) và điểm M nằm ngoài đường tròn. Qua M kẻ các tiếp tuyến MA, MB
Câu hỏi:
Cho đường tròn (O) và điểm M nằm ngoài đường tròn. Qua M kẻ các tiếp tuyến MA, MB với đường tròn (O) với A, B là các tiếp điểm. Chứng minh 4 điểm A, B, O, M cùng thuộc một đường tròn.
Trả lời:
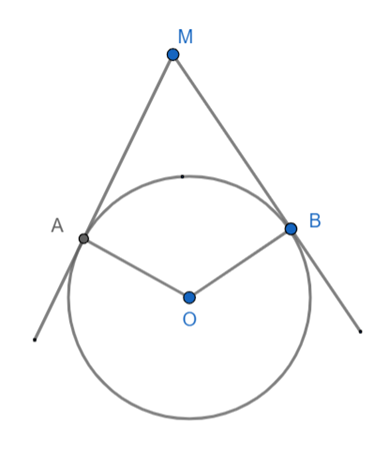
Ta có: \(\widehat {MAO} = 90^\circ \)(vì MA là tiếp tuyến của (O) nên MA ⊥ OA)
\(\widehat {MBO} = 90^\circ \)(vì MA là tiếp tuyến của (O) nên MA ⊥ OA)
Xét tứ giác AMBO có:
\(\widehat {MAO} + \widehat {MBO} = 90^\circ + 90^\circ = 180^\circ \)
Suy ra: tứ giác AMBO nội tiếp đường tròn vì có tổng 2 góc đối bằng 180°
Vậy A, M, B, O cùng thuộc 1 đường tròn.

