Cho đường tròn tâm O bán kính R, dây BC khác đường kính. Hai tiếp tuyến của

Cho đường tròn tâm O bán kính R, dây BC khác đường kính. Hai tiếp tuyến của đường tròn (O, R) tại B và tại C cắt nhau tại A. Kẻ đường kính CD, kẻ BH vuông góc với CD tại H.

a) Chứng minh bốn điểm A, B, O, C cùng thuộc một đường tròn. Xác định tâm và bán kính của đường tròn đó.

b) Chứng minh AO vuông góc với BC. Cho biết R = 15 cm, BC = 24cm. Tính AB, OA.

c) Chứng minh BC là tia phân giác của góc ABH

d) Gọi I là giao điểm của AD và BH, E là giao điểm của BD và AC. Chứng minh IH = IB.

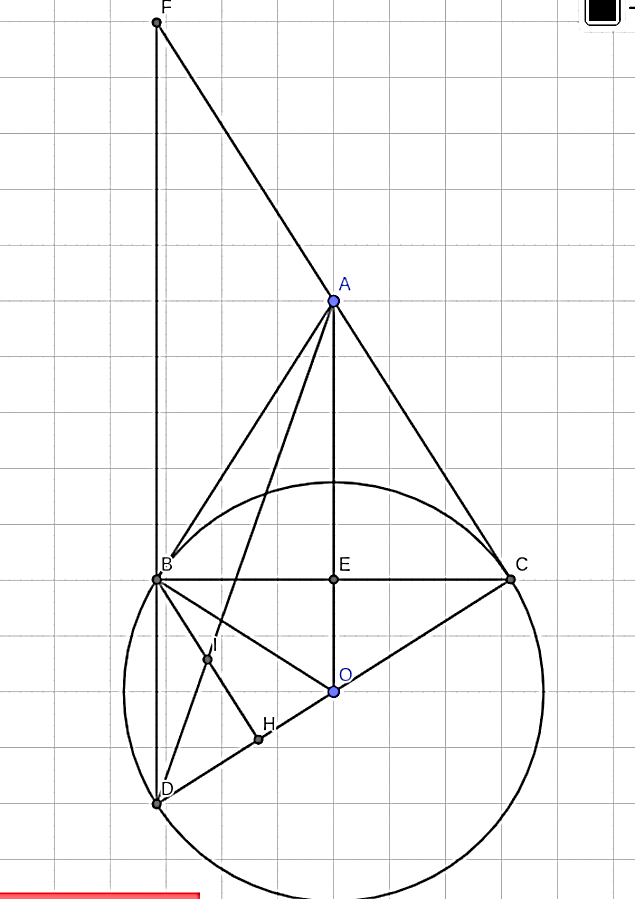
a) Ta có AB, AC là tiếp tuyến của (O) ⇒ $\widehat{ABO}=\widehat{ACO}$ = 90°

⇒ $\widehat{ABO}+\widehat{ACO}$ = 90° + 90° = 180°

⇒ A, B, O, C cùng thuộc đường tròn đường kính (AO).

b) Vì AB, AC là tiếp tuyến của (O)

⇒ AB = AC (tính chất hai tiếp tuyến cắt nhau)

và có OB = OC nên AO là đường trung trực của BC
⇒AO ⊥ BC

Gọi AO ∩ BC = E

⇒ E là trung điểm BC
⇒ BE = $\frac{1}{2}BC$

Do AB ⊥ OB, BE ⊥ AO

Áp dụng hệ thức lượng vào Δ vuông ABO đường cao BE có:

$\frac{1}{B{E}^2}=\frac{1}{O{B}^2}+\frac{1}{B{A}^2}$⇒ AB = 20

⇒ OA² = AB² + OB² = 625⇒AO = 25

c) Ta có:
BH ⊥ OC ⇒ BH//AC ⇒ $\widehat{HBC}=\widehat{ACB}=\widehat{ABC}$

⇒ BC là phân giác  $\widehat{ABH}$

d) Gọi BD ∩ AC = F

Ta có: FB ⊥ BC, AB = AC

⇒ A là trung điểm CF 

⇒ AF = AC
Mà BH ⊥ CD

⇒ BH // CF

⇒ $\frac{BI}{AF}=\frac{DI}{DA}=\frac{IH}{AC}$

⇒ IB = IH.