Cho hai đường tròn (O) và (O’) tiếp xúc trong tại A. Qua A vẽ dây AB, AC của đường tròn (O), chúng cắt (O’) theo thứ tự tại D và E. Chứng minh BC // DE.
Câu hỏi:
Cho hai đường tròn (O) và (O’) tiếp xúc trong tại A. Qua A vẽ dây AB, AC của đường tròn (O), chúng cắt (O’) theo thứ tự tại D và E. Chứng minh BC // DE.
Trả lời:
Lời giải
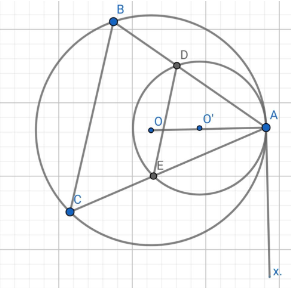
Vì (O) và (O’) tiếp xúc trong tại A.
Suy ra A thuộc đường nối tâm OO’.
Qua A, vẽ tiếp tuyến Ax chung của hai đường tròn (O) và (O’).
Xét đường tròn (O’), có: \(\widehat {EAx} = \widehat {EDA} = \frac{1}{2}\)sđ (1)
Xét đường tròn (O), có: \(\widehat {CAx} = \widehat {CBA} = \frac{1}{2}\)sđ (2)
Ta có \(\widehat {EAx} = \widehat {CAx}\) (3)
Từ (1), (2), (3), suy ra \(\widehat {CBA} = \widehat {EDA}\).
Mà hai góc này ở vị trí đồng vị.
Vậy BC // DE (điều phải chứng minh).
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Biết rằng \(\mathop {\lim }\limits_{x \to 0} \frac{{\sin x}}{x} = 1\). Tìm giá trị thực của tham số m để hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{1 + \cos x}}{{{{\left( {x - \pi } \right)}^2}}},\,\,\,\,\,\,x \ne \pi \\m,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = \pi \end{array} \right.\) liên tục tại x = π.
Xem lời giải »
Câu 2:
Có bao nhiêu số tự nhiên nhỏ hơn 100 chia hết cho 2 và 3.
Xem lời giải »
Câu 3:
Chứng minh rằng với mọi góc α (0° ≤ α ≤ 180°), ta đều có sin2α + cos2α = 1.
Xem lời giải »
Câu 6:
Trước nửa đêm là bao nhiêu phút nếu trước đó 32 phút thời gian này gấp 3 lần số phút sau 22 giờ?
Xem lời giải »
Câu 7:
Một cửa hàng bán trái cây nhập khẩu 500 kg cam với giá 40 000 đồng/kg. Phí vận chuyển của chuyến hàng là 4 000 000 đồng. Giả sử rằng 10% số kg cam trên bị hư trong quá trình vận chuyển và số kg cam còn lại được bán hết. Hỏi giá bán của mỗi kg cam là bao nhiêu để công ty có lợi nhuận 20% so với tiền vốn ban đầu?
Xem lời giải »
Câu 8:
Cho tam giác ABC vuông tại A, có AH là đường cao, AM là đường trung tuyến. Qua B kẻ đường thẳng vuông góc với AM tại I cắt AC tại E.
a) Chứng minh BI.BE = 2BH.BM.
b) Chứng minh \(\frac{1}{{A{B^2}}} = \frac{1}{{B{E^2}}} + \frac{1}{{B{C^2}}}\).
Xem lời giải »


