Chứng minh rằng với mọi góc α (0° ≤ α ≤ 180°), ta đều có sin^2α + cos^2α = 1.
Câu hỏi:
Chứng minh rằng với mọi góc α (0° ≤ α ≤ 180°), ta đều có sin2α + cos2α = 1.
Trả lời:
Lời giải
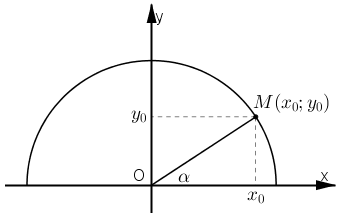
Vẽ đường tròn lượng giác (O; 1).
Với mọi α (0° ≤ α ≤ 180°), ta đều có điểm M(x0; y0) thuộc nửa đường tròn sao cho \(\widehat {MOx} = \alpha \).
Khi đó ta có: sinα = y0 và cosα = x0.
Mà M thuộc đường tròn lượng giác nên \(x_0^2 + y_0^2 = O{M^2}\).
⇔ sin2α + cos2α = 1.
Vậy ta có điều phải chứng minh.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Biết rằng \(\mathop {\lim }\limits_{x \to 0} \frac{{\sin x}}{x} = 1\). Tìm giá trị thực của tham số m để hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{1 + \cos x}}{{{{\left( {x - \pi } \right)}^2}}},\,\,\,\,\,\,x \ne \pi \\m,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = \pi \end{array} \right.\) liên tục tại x = π.
Xem lời giải »
Câu 2:
Có bao nhiêu số tự nhiên nhỏ hơn 100 chia hết cho 2 và 3.
Xem lời giải »
Câu 4:
Trong lớp 10C có 16 học sinh giỏi Toán, 15 học sinh giỏi Lí, 11 học sinh giỏi Hóa. Biết rằng có 9 học sinh vừa giỏi Toán và Lí, 6 học sinh vừa giỏi Lí và Hóa, 8 học sinh vừa giỏi Hóa và Toán, trong đó có 11 học sinh giỏi đúng 2 môn. Hỏi có bao nhiêu học sinh trong lớp:
a) Giỏi cả ba môn.
b) Giỏi đúng 1 môn.
Xem lời giải »
Câu 5:
Có bao nhiêu số tự nhiên có 9 chữ số mà các chữ số của nó viết theo thứ tự giảm dần?
Xem lời giải »


