Cho hàm số y = f(x) có đồ thị như hình vẽ bên. Có bao nhiêu giá trị nguyên của
Câu hỏi:
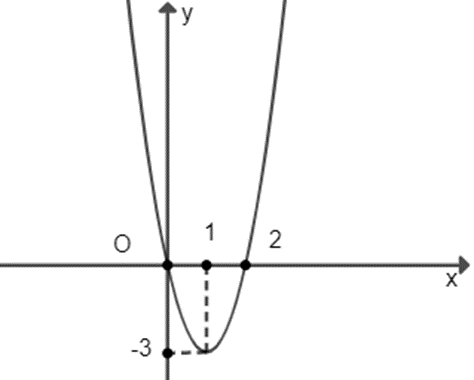
Cho hàm số y = f(x) có đồ thị như hình vẽ bên. Có bao nhiêu giá trị nguyên của tham số m để phương trình f[f(x) + m] = 0 có đúng 3 nghiệm phân biệt.
A. 1;
B. 2;
C. 3;
D. 4.
Trả lời:
Đáp án đúng là: A
Đặt f(x) = t (*)
Nhận xét:
• Với phương trình t = −3 có một nghiệm x = 1.
• Với t > −3 nên phương trình (*) có hai nghiệm x = x1 và x = x2 với x1 < 1; x2 > 1
Ta có f [f(x) + m] = 0 \( \Leftrightarrow \left[ \begin{array}{l}t + m = 0\\t + m = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}t = - m\\t = 2 - m\end{array} \right.\)
Vì 2 – m > −m, \(\forall \)m nên f [f(x) + m] = 0 có đúng 3 nghiệm phân biệt khi và chỉ khi:
\(\left\{ \begin{array}{l} - m = - 3\\2 - m > - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = 3\\m < 5\end{array} \right. \Leftrightarrow m = 3\)
Vậy có 1 giá trị nguyên của m thỏa mãn yều cầu bài toán.

