Cho hàm số y= x^4- 2( 1-m^2)x^2+ m+1. Tồn tại giác trị của m để hàm số có cực đại, cực tiểu

Câu hỏi:

Cho hàm số y= x⁴- 2( 1-m²) x²+ m+1. Tồn tại giác trị của m  để  hàm số có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số lập thành tam giác có diện tích lớn nhất . Khi đó khẳng định nào đúng?

A. m là số nguyên dương

B. m không là số nguyên

C. m= 1

D. Tất cả sai

Trả lời:

Ta có đạo hàm y’ = 4x³- 4( 1-m²) x

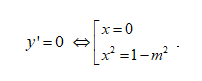
Hàm số có cực đại , cực tiểu khi và chỉ khi -1< m <1  

Tọa độ điểm cực trị 

$$\begin{gathered} A(0;m+1); B(\sqrt{1-m^2};-m^4+2m^2+m); C(-\sqrt{1-m^2};-m^4+2m^2+m); \\ \overrightarrow{BC}=(-2\sqrt{1-m^2};0) \end{gathered}$$

Phương trình đường thẳng BC: y + m⁴- 2m²- m=0

d( A, BC) = m⁴-2m²+ 1,

$$\begin{gathered} BC=2\sqrt{1-m^2} \\ \Rightarrow S_{∆ABC} =\frac{1}{2}BC.d\left[A,BC\right] \\ =\sqrt{1-m^2}(m^4-2m^2+1)=\sqrt{{(1-m^2)}^5}\le 1 \end{gathered}$$

Vậy S đạt giá trị lớn nhất bằng 1 khi và chỉ khi m= 0.

Chọn D.