Tập nghiệm của bất phương trình: 5x − 1 + x + 3 ≥ 4 có bao nhiêu giá trị nguyên trong ( 0; 2008]
Câu hỏi:
Tập nghiệm của bất phương trình: có bao nhiêu giá trị nguyên trong ( 0; 2008]
A.2006
B. 2001
C. 2008
D. 2007
Trả lời:
Điều kiện: x≥ 1/5
Xét hàm số: liên tục trên nửa khoảng .
Ta có: 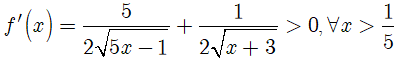
Do đó hàm số f( x) là hàm số đồng biến trên .
Mặt khác : f(1) =4
Khi đó bất phương trình đã cho trở thành f(x) ≥ f(1) hay x≥1.
Ta thấy từ (0 ; 2008] có các giá trị của x thỏa mãn là : 1 ;2 ;3 ;4....2008.
Chọn C.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho hàm số y= x3-3x2-m-1 có đồ thị (C) . Giá trị của tham số m để đồ thị (C) cắt trục hoành tại ba điểm phân biệt lập thành cấp số cộng là
Xem lời giải »
Câu 2:
Tìm tất cả các giá trị thực của tham số m sao cho hàm số đồng biến trên khoảng ?
Xem lời giải »
Câu 3:
Cho hàm số có đồ thị (C) và đường thẳng d: y=x+m. Đường thẳng d cắt đồ thị (C) tại hai điểm A và B. Với C( -2; 5) , giá trị của tham số m để tam giác ABC đều là
Xem lời giải »
Câu 4:
Bất phương trình có tập nghiệm là [a; b]. Hỏi tổng a2+ b2 có giá trị là bao nhiêu?
Xem lời giải »
Câu 5:
Bất phương trình có tập nghiệm là ( a; b]. Hỏi 4a-b có giá trị là bao nhiêu?
Xem lời giải »
Câu 6:
Cho hàm số: y = x3+2mx2+3(m-1)x+2 có đồ thị (C) . Đường thẳng d: y= - x+2 cắt đồ thị (C) tại ba điểm phân biệt A(0; -2); B và C. Với M(3;1) giá trị của tham số m để tam giác MBC có diện tích bằng là
Xem lời giải »

