Cho hình chóp S.ABCD có đáy ABCD là hình thang, AD // BC và AD = 2BC. Lấy M trên cạnh SA sao cho MA = 2MS.
Câu hỏi:
Cho hình chóp S.ABCD có đáy ABCD là hình thang, AD // BC và AD = 2BC. Lấy M trên cạnh SA sao cho MA = 2MS.
a) Chứng minh OM // (SCD).
b) Xác định giao điểm N của MD và mặt phẳng (SBC).
Trả lời:
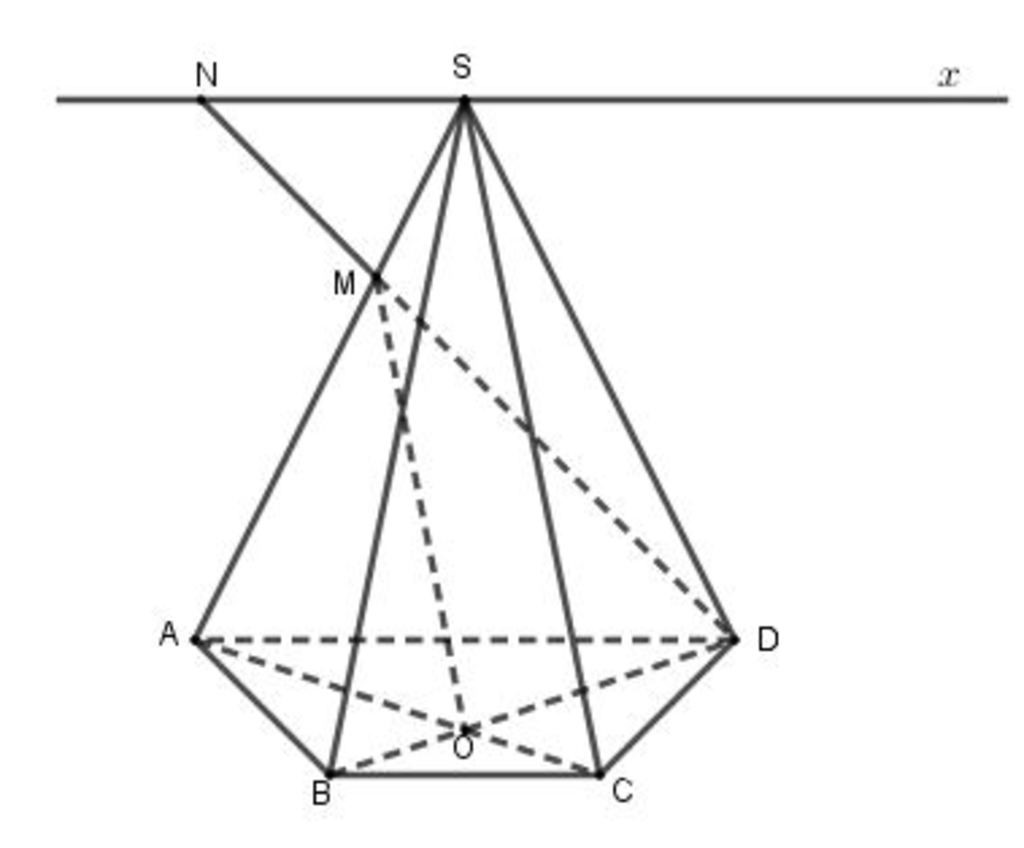
Do AD // BC nên
Mà nên
⇒OM // SC (định lí Ta–let)
Lại có SC ⊂ (SCD) nên OM//(SCD)
b) Ta có: MD ⊂ (SAD)
* Tìm giao tuyến của (SBC) với (SAD)
Ta có: S ∈ (SAD) ∩ (SBC)
Lại có: ⇒ (SAD) ∩ (SBC) = Sx // AD // BC.
Do đó giao tuyến của (SBC) với (SAD) là đường thẳng đi qua S và song song với AD, BC.
Trong mặt phẳng (SAD), gọi N là giao điểm của MD với Sx.
Khi đó ⇒ N = MD ∩ (SBC).
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Giải phương trình: (x – 1)(x – 2)(x – 3)(x – 4) = 120.
Xem lời giải »
Câu 2:
Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của BC, CA, AB. Chứng minh rằng: .
Xem lời giải »
Câu 3:
Cho ABC vuông tại A có AB < AC. Gọi D, E lần lượt là trung điểm của các cạnh BC và AC. Trên tia đối của tia DE lấy điểm F sao cho D là trung điểm của cạnh EF.
a) Chứng minh tứ giác BFCE là hình bình hành.
b) Chứng minh tứ giác BFEA là hình chữ nhật.
c) Gọi K là điểm đối xứng với F qua E. Chứng minh tứ giác AFCK là hình thoi.
d) Vẽ AH ⊥ BC tại H. Gọi M là trung điểm của HC. Chứng minh FM ⊥ AM.
Xem lời giải »
Câu 4:
Có 3 bì thư giống nhau lần lượt được đánh số thứ tự từ 1 đến 3 và 3 con tem giống nhau lần lượt đánh số thứ tự từ 1 đến 3. Dán 3 con tem đó vào 3 bì thư sao cho không có bì thư nào không có tem. Tính xác suất để lấy ra được 2 bì thư trong 3 bì thư trên sao cho mỗi bì thư đều có số thứ tự giống với số thứ tự con tem đã dán vào nó
Xem lời giải »
Câu 5:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông bằng cạnh bằng a, tam giác SAB là tam giác đều, SC = SD = . Tính thể tích V của khối chóp S.ABCD?
Xem lời giải »
Câu 6:
Cho sin α = với 90° < α < 180°. Tính cos2α + 3tan2α.
Xem lời giải »
Câu 7:
Cho tam giác ABC có hai trung tuyến BD và CE cắt nhau tại G. Gọi M ,N theo thứ tự là trung điểm của BG và CG.
a, Chứng minh tứ giác MNDE là hình bình hành .
b, Tìm điều kiện của tam giác ABC để MNDE là hình chữ nhật.
Xem lời giải »
Câu 8:
Cho tam giác ABC có đường cao AD, và trực tâm H. Gọi I, K lần lượt là trung điểm của HA, HB. Gọi E, F lần lượt là trung điểm của BC, AC. Chứng minh
a) Bốn điểm E, F, I, K cùng thuộc một đường tròn.
b) Điểm D cũng thuộc đường tròn đi qua bốn điểm E, F, I, K.
Xem lời giải »


