Cho tam giác ABC có hai trung tuyến BD và CE cắt nhau tại G. Gọi M ,N theo thứ tự là trung điểm của BG
Câu hỏi:
Cho tam giác ABC có hai trung tuyến BD và CE cắt nhau tại G. Gọi M ,N theo thứ tự là trung điểm của BG và CG.
a, Chứng minh tứ giác MNDE là hình bình hành .
b, Tìm điều kiện của tam giác ABC để MNDE là hình chữ nhật.
Trả lời:
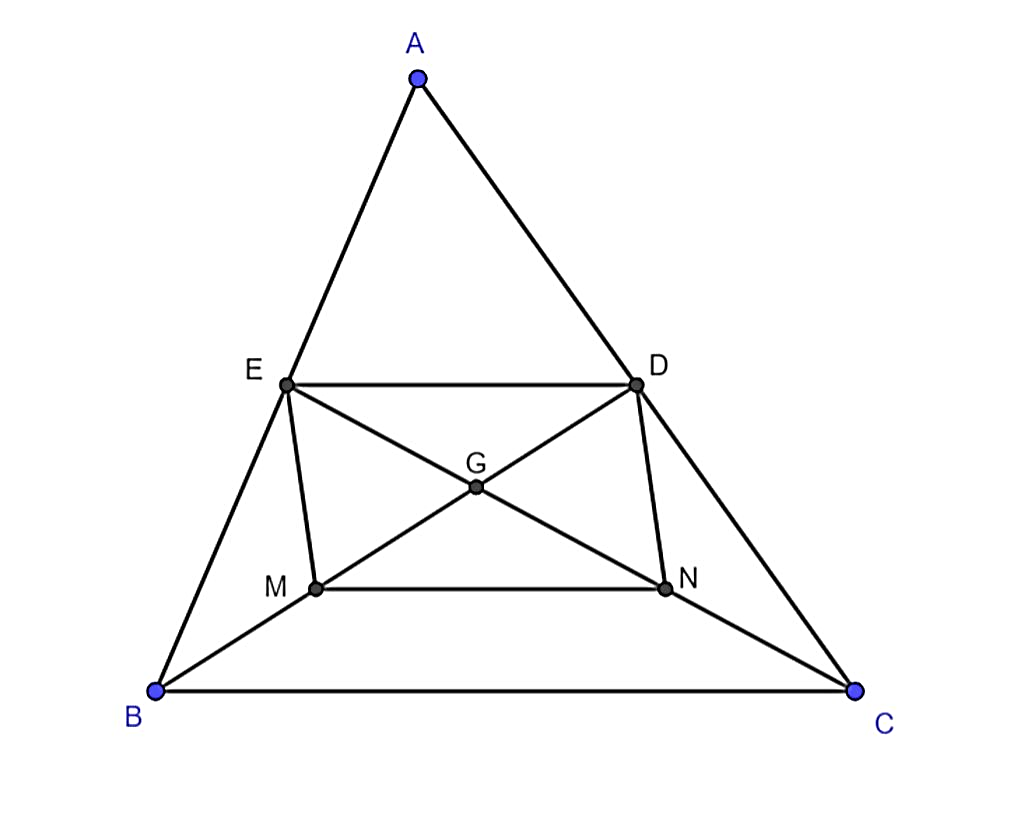
Xét tam giác ABC có AE = EB (gt), AD = DC (gt)
⇒ ED là đường trung bình của tam giác ABC
⇒ ED // BC và ED = BC
Xét tam giác BGC có BM = MG (gt), CN = NG (gt)
⇒ MN là đường trung bình của tam giác BGC
⇒ MN // BC và MN = BC
Có MN // BC mà ED // BC ⇒ MN//ED
MN = BC, ED = BC ⇒ MN = ED
Tứ giác MNDE có: MN // ED, MN = ED
⇒ MNDE là hình bình hành
b, Hình bình hành MNDE là hình chữ nhật
⇔ = 90°
Nếu = 90°
⇒ BD vừa là trung tuyến vừa là đường cao của tam giác ABC ứng với AC
⇒Tam giác ABC cân tại B
Vậy, để hình bình hành MNDE là hình chữ nhật, tam giác ABC phải cân tại B.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Giải phương trình: (x – 1)(x – 2)(x – 3)(x – 4) = 120.
Xem lời giải »
Câu 2:
Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của BC, CA, AB. Chứng minh rằng: .
Xem lời giải »
Câu 3:
Cho ABC vuông tại A có AB < AC. Gọi D, E lần lượt là trung điểm của các cạnh BC và AC. Trên tia đối của tia DE lấy điểm F sao cho D là trung điểm của cạnh EF.
a) Chứng minh tứ giác BFCE là hình bình hành.
b) Chứng minh tứ giác BFEA là hình chữ nhật.
c) Gọi K là điểm đối xứng với F qua E. Chứng minh tứ giác AFCK là hình thoi.
d) Vẽ AH ⊥ BC tại H. Gọi M là trung điểm của HC. Chứng minh FM ⊥ AM.
Xem lời giải »
Câu 4:
Có 3 bì thư giống nhau lần lượt được đánh số thứ tự từ 1 đến 3 và 3 con tem giống nhau lần lượt đánh số thứ tự từ 1 đến 3. Dán 3 con tem đó vào 3 bì thư sao cho không có bì thư nào không có tem. Tính xác suất để lấy ra được 2 bì thư trong 3 bì thư trên sao cho mỗi bì thư đều có số thứ tự giống với số thứ tự con tem đã dán vào nó
Xem lời giải »
Câu 5:
Cho tam giác ABC có đường cao AD, và trực tâm H. Gọi I, K lần lượt là trung điểm của HA, HB. Gọi E, F lần lượt là trung điểm của BC, AC. Chứng minh
a) Bốn điểm E, F, I, K cùng thuộc một đường tròn.
b) Điểm D cũng thuộc đường tròn đi qua bốn điểm E, F, I, K.
Xem lời giải »
Câu 6:
Cho tam giác ABC, N là điểm xác định bởi , G là trọng tâm tam giác ABC. Hệ thức tính theo và là?
Xem lời giải »
Câu 7:
Cho tập hợp A={1;2;3;...;n} trong đó n là số nguyên dương lớn hơn 1. Hỏi có bao nhiêu cặp sắp thứ tự (x;y) thõa mãn: x và y thuộc A; x lớn hơn y?
Xem lời giải »
Câu 8:
Cho véc tơ . Với giá trị nào của y thì véc tơ tạo với véc tơ một góc 45°.
Xem lời giải »


