Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. SA = a và SA vuông góc với đáy. Tính khoảng cách d giữa hai đường chéo nhau SC và BD.
Câu hỏi:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. SA = a và SA vuông góc với đáy. Tính khoảng cách d giữa hai đường chéo nhau SC và BD.
Trả lời:
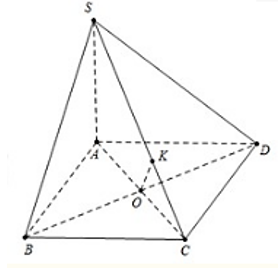
Gọi O là tâm hình vuông ABCD
Ta có: AC ^ BD; BD ^ SA
Do đó BD ^ (SAC)
Dựng OK ^ SC
Do đó OK là đoạn vuông góc chung của BD và SC
Khi đó (1)
Ta có: AC2 = AB2 + BC2 = 2a2
Suy ra
Thay vào (1) ta có .
Vậy .

