Cho hình chóp S.ABCD đáy là hình thang (đáy lớn AB). Gọi M, N là trung điểm BC; SB. P thuộc AD sao cho
Câu hỏi:
Cho hình chóp S.ABCD đáy là hình thang (đáy lớn AB). Gọi M, N là trung điểm BC; SB. P thuộc AD sao cho 2PD = PA. Chứng minh MN // (SCD), tìm giao điểm của SA và (MNP).
Trả lời:
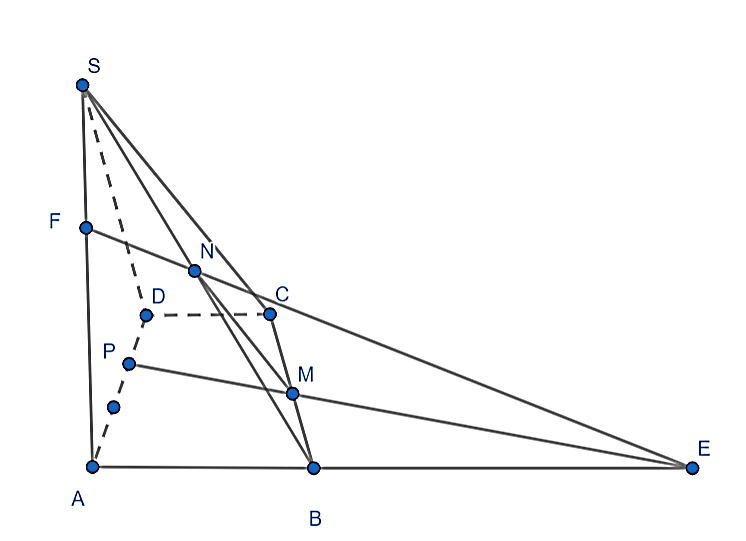
Ta có: M, N là trung điểm BC; SB nên MN là đường trung bình của tam giác SCB
Suy ra: MN // SC
Mà SC ∈ (SCD) nên MN // (SCD)
+) Gọi giao điểm của PM và AB là E
Ta có: E ∈ AB ⸦ (SAB), E ∈ PM ⸦ (MNP)
Giao điểm của EN và SA là F
Mà EN ⸦ (MNP)
Suy ra: SA ∩ (MNP) = {F}.

