Cho hình chóp tam giác đều S.ABC có các cạnh bên SA, SB, SC vuông góc với nhau từng đôi một. Biết thể tích của khối chóp bằng . Tính bán kính r của mặt cầu nội tiếp của hình chóp S.ABC.
Câu hỏi:
Cho hình chóp tam giác đều S.ABC có các cạnh bên SA, SB, SC vuông góc với nhau từng đôi một. Biết thể tích của khối chóp bằng a36. Tính bán kính r của mặt cầu nội tiếp của hình chóp S.ABC.
Trả lời:
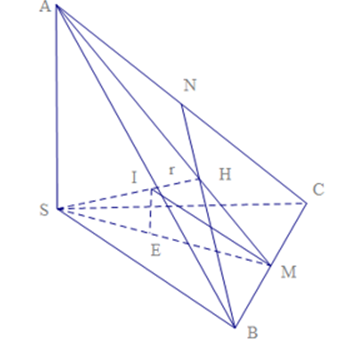
Áp dụng công thức r=3VStp (*) và tam giác đều cạnh x có diện tích S=x2√34
Từ giả thiết S.ABC đều có SA = SB = SC.
Lại có SA, SB, SC đôi một vuông góc và thể tích khối chóp S.ABC bằng a36nên ta có SA = SB = SC = a.
Suy ra AB=BC=CA=a√2 và tam giác ABC đều cạnh có độ dài a√2.
Do đó diện tích toàn phần của khối chóp S.ABC là:
Stp = SSAB + SSBC + SSCA + SABC
=3a22+(a√2)2.√34=a2(3+√3)2
Thay vào (*) ta được:
4π3
Vậy r = r=a3+√3.
