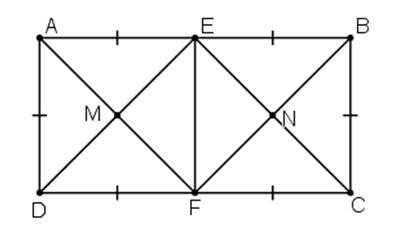
Cho hình chữ nhật ABCD có AB = 2AD. Gọi E, F theo thứ tự là trung diểm của AB, CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE. Tứ giác ADFE là hình gì? Vì sao?

Tìm x:

x : 0,25 + x ´ 11 = 24

Tìm x:

x ´ 8,01 – x : 100 = 38

Cho tam giác ABC vuông tại A. Đường cao AH. Kẻ phân giác của $\widehat{ACH}$ cắt AH tại M, kẻ phân giác của $\widehat{BAH}$ cắt BH tại N. Chứng minh rằng MN // AB.

Tìm x:

x × 9,8 – x : 0,25 = 18,096

Cho hình chữ nhật ABCD có AB = 2AD. Gọi E, F theo thứ tự là trung diểm của AB, CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE. Tứ giác EMFN là hình gì? Vì sao?

Cho nửa đường tròn tâm O đường kính AB. Ax là tia tiếp tuyến của nửa đường tròn (Ax và nửa đường tròn cùng thuộc một nửa mặt phẳng bờ AB), từ điểm C trên nửa đường tròn (C khác A, B) vẽ tiếp tuyến CM cắt Ax tại M, hạ CH vuông góc với AB, MB cắt (O) tại Q và cắt CH tại N. Chứng minh MA² = MQ . MB

Cho tam giác ABC cân tại A, I là giao điểm các đường phân giác trong tam giác. Chứng minh AC là tiếp tuyến của đường tròn tâm O ngoại tiếp tam giác BIC.