Cho tam giác ABC cân tại A, I là giao điểm các đường phân giác trong tam giác. Chứng minh AC là tiếp tuyến của đường tròn tâm O ngoại tiếp tam giác BIC.
Câu hỏi:
Cho tam giác ABC cân tại A, I là giao điểm các đường phân giác trong tam giác. Chứng minh AC là tiếp tuyến của đường tròn tâm O ngoại tiếp tam giác BIC.
Trả lời:
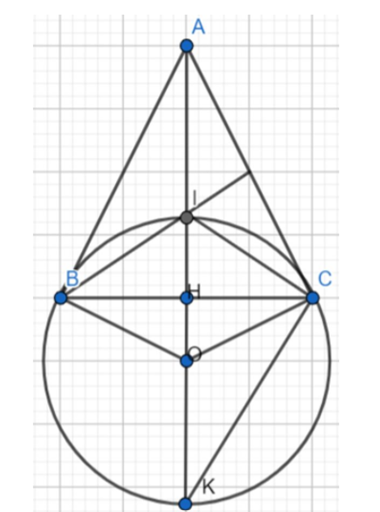
Vì ΔABC cân tại A nên AI vừa là đường phân giác vừa là đường cao
Do đó ba điểm A, I, O thẳng hàng
Þ AO ⊥ BC
(1)
Vì OI = OC = R nên ΔIOC cân tại O
(2)
CI là phân giác của :
(3)
Từ (1); (2) và (3) ta có:
Þ AC ^ CO
Vậy AC là tiếp tuyến của đường tròn tâm O ngoại tiếp tam giác BIC.

