Cho hình chữ nhật ABCD, vẽ tam giác AEC vuông tại E. Chứng minh rằng 5 điểm A, B, C, D, E
Câu hỏi:
Cho hình chữ nhật ABCD, vẽ tam giác AEC vuông tại E. Chứng minh rằng 5 điểm A, B, C, D, E cùng thuộc một đường tròn.
Trả lời:
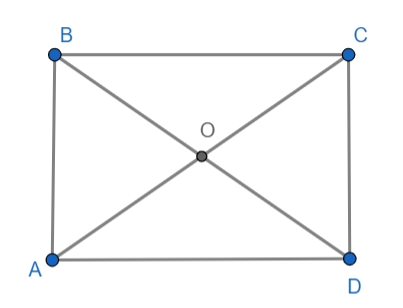
Gọi giao điểm của AC và BD là O.
Vì ABCD là hình chữ nhật nên tứ giác ABCD nội tiếp một đường tròn
Xét tứ giác ADEC có:
hay
Suy ra: ADEC nội tiếp đường tròn .
Qua 3 điểm không thẳng hàng chỉ xác định duy nhất 1 và chỉ 1 đường tròn
Do đó: A, B, C, D, E cùng thuộc một đường tròn.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Giải phương trình: (x – 1)(x – 2)(x – 3)(x – 4) = 120.
Xem lời giải »
Câu 2:
Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của BC, CA, AB. Chứng minh rằng: .
Xem lời giải »
Câu 3:
Cho ABC vuông tại A có AB < AC. Gọi D, E lần lượt là trung điểm của các cạnh BC và AC. Trên tia đối của tia DE lấy điểm F sao cho D là trung điểm của cạnh EF.
a) Chứng minh tứ giác BFCE là hình bình hành.
b) Chứng minh tứ giác BFEA là hình chữ nhật.
c) Gọi K là điểm đối xứng với F qua E. Chứng minh tứ giác AFCK là hình thoi.
d) Vẽ AH ⊥ BC tại H. Gọi M là trung điểm của HC. Chứng minh FM ⊥ AM.
Xem lời giải »
Câu 4:
Có 3 bì thư giống nhau lần lượt được đánh số thứ tự từ 1 đến 3 và 3 con tem giống nhau lần lượt đánh số thứ tự từ 1 đến 3. Dán 3 con tem đó vào 3 bì thư sao cho không có bì thư nào không có tem. Tính xác suất để lấy ra được 2 bì thư trong 3 bì thư trên sao cho mỗi bì thư đều có số thứ tự giống với số thứ tự con tem đã dán vào nó
Xem lời giải »
Câu 6:
Hai người đi xe từ A đến C. Người thứ nhất đi theo đường từ A đến B rồi từ B đến C. Người thứ hai đi thẳng từ A đến C. Cả hai đều về đích cùng lúc. Tính quãng đường và độ dịch chuyển của người thứ nhất và người thứ hai, so sánh và nhận xét kết quả.
Xem lời giải »
Câu 7:
Tam giác ABC có AC = 4, = 60°. Tính độ dài đường cao h xuất phát từ đỉnh A của tam giác.
Xem lời giải »


