Cho hình vuông ABCD cạnh a. Gọi M, N lần lượt thuộc đoạn BC, AC sao cho
Câu hỏi:
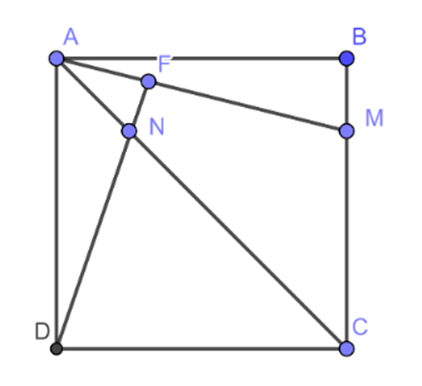
Cho hình vuông ABCD cạnh a. Gọi M, N lần lượt thuộc đoạn BC, AC sao cho: \(\overrightarrow {BM} = \frac{1}{3}\overrightarrow {MC} ;\overrightarrow {CN} = k\overrightarrow {AN} \). Tìm k sao cho AM vuông góc với DN.
Trả lời:
\(\overrightarrow {BM} = \frac{1}{3}\overrightarrow {MC} \Rightarrow \overrightarrow {BM} = \frac{1}{4}\overrightarrow {BC} \)
\(\overrightarrow {CN} = k\overrightarrow {AN} \Rightarrow \overrightarrow {CN} = - k\overrightarrow {NA} \Rightarrow \overrightarrow {CA} = \left( {1 - k} \right)\overrightarrow {NA} \Rightarrow \overrightarrow {AN} = \frac{1}{{1 - k}}\overrightarrow {AC} \)
AM vuông góc với DN khi và chỉ khi: \(\overrightarrow {AM} .\overrightarrow {DN} = 0\)
⇔ \(\left( {\overrightarrow {AB} + \overrightarrow {BM} } \right).\left( {\overrightarrow {DA} + \overrightarrow {AN} } \right) = 0\)
⇔\(\left( {\overrightarrow {AB} + \frac{1}{4}\overrightarrow {BC} } \right).\left( {\overrightarrow {DC} + \frac{1}{{1 - k}}\overrightarrow {AC} } \right) = 0\)
⇔\[\overrightarrow {AB} .\overrightarrow {DC} + \frac{1}{{1 - k}}.\overrightarrow {AB} .\overrightarrow {DC} + \frac{1}{4}\overrightarrow {BC} .\overrightarrow {DC} + \frac{1}{4}.\frac{1}{{1 - k}}.\overrightarrow {BC} .\overrightarrow {AC} = 0\]
⇔ \[a.a.\cos 0^\circ + \frac{1}{{1 - k}}.a.a\sqrt 2 .\cos 45^\circ + \frac{1}{4}.a.a.\cos 90^\circ + \frac{1}{4}.\frac{1}{{1 - k}}.a.a\sqrt 2 .\cos 45^\circ = 0\]
⇔\[{a^2} + \frac{{{a^2}}}{{1 - k}} + \frac{{{a^2}}}{{4\left( {1 - k} \right)}} = 0\]
⇔ \[{a^2}\left( {1 + \frac{1}{{1 - k}} + \frac{1}{{4\left( {1 - k} \right)}}} \right) = 0\]
⇔ \[\frac{{4 - 4k + 4 + 1}}{{4\left( {1 - k} \right)}} = 0\]
⇔ –4k + 9 = 0
⇔ k = \(\frac{9}{4}\).

