Cho hình vuông ABCD. Lấy điểm M thuộc cạnh AC. Kẻ MH, MK lần lượt vuông góc với DA, DC. Chứng minh BM vuông góc với HK.

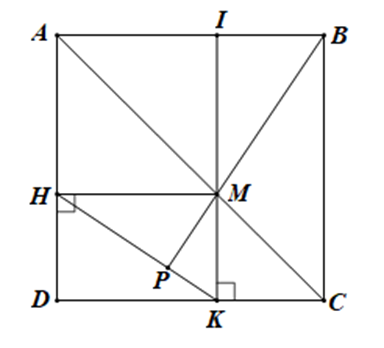
Gọi I là giao điểm của MK và AB, P là giao điểm của BM và HK.

Xét tứ giác AIMH có: $\widehat{A}=\widehat{AHM}=\widehat{AIM}=90°$ nên là AIMH là hình chữ nhật

Lại có AM là phân giác của góc A nên AIMH là hình vuông.

Suy ra HM = IM = IA.

Lại có IBCK là hình chữ nhật (do có 3 góc vuông) nên IK = BC = AB

Khi đó IK – IM = AB – IA hay MK = IB.

Xét DHMK và DMIB có:

$\widehat{HMK}=\widehat{MIB}=90°$;

HM = IM (cmt);

MK = IB (cmt)

Suy ra DHMK = DMIB (hai cạnh góc vuông)

Do đó $\widehat{MBI}=\widehat{HKM}$ (hai góc tương ứng)

Lại có $\widehat{MBI}+\widehat{BMI}=90°$ (hai góc nhọn phụ nhau trong DMIB vuông tại I)

và $\widehat{BMI}=\widehat{PMK}$ (đối đỉnh)

Suy ra $\widehat{HKM}+\widehat{PMK}=90°$, do đó $\widehat{MPK}=90°$

Vậy BM ⊥ HK.