Cho tam giác ABC cân tại A, đường cao CD. Chứng minh rằng: AB2 + BC2 + AC2 = BD2 + 2AD2 + 3CD2.
Câu hỏi:
Cho tam giác ABC cân tại A, đường cao CD. Chứng minh rằng: AB2 + BC2 + AC2 = BD2 + 2AD2 + 3CD2.
Trả lời:
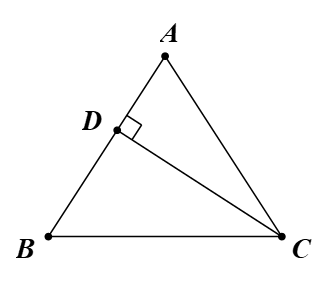
Áp dụng định lí Pytago cho tam giác ACD vuông tại D: AD2 + CD2 = AC2 (1)
⇔ AD2 + CD2 = AB2 (do tam giác ABC cân tại A nên AB = AC) (2)
Áp dụng định lí Pytago cho tam giác DBC vuông tại D: BD2 + CD2 = BC2 (3)
Lấy (1) + (2) + (3) vế theo vế, ta được: BD2 + 2AD2 + 3CD2 = AB2 + BC2 + AC2.
Vậy ta có điều phải chứng minh.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Một đơn vị bộ đội dự trữ gạo đủ cho 150 người ăn trong 20 ngày. Nhưng sau đó lại có thêm một số bộ đội chuyển đến nên số ngày ăn hết số gạo dự trữ giảm đi 8 ngày. Hỏi có bao nhiêu bộ đội mới chuyển đến?
Xem lời giải »
Câu 2:
Mùng 1 tháng 1 năm 2015 là thứ 5. Hỏi ngày mùng 1 tháng 1 năm 2016 là thứ mấy?
Xem lời giải »
Câu 3:
Số bị chia hơn số chia 60 đơn vị. Nếu giảm số chia đi một nửa thì thương mới là 32. Tìm số bị chia và số chia lúc đầu.
Xem lời giải »
Câu 4:
Tuổi của An trước đây 3 năm bằng tuổi của An sau 3 năm nữa. Tính tuổi của An hiện nay.
Xem lời giải »
Câu 5:
Xác định a, b để A = x3 – 5bx + 2a chia hết cho B = (x + 2)2.
Xem lời giải »
Câu 6:
Tìm a, b, c để f(x) = 2x4 + ax2 + bx + c chia hết cho x + 2 và f(x) chia cho x2 – 1 dư x.
Xem lời giải »
Câu 7:
Cho tam giác ABC vuông tại A (AB < AC) có AH là đường cao. Gọi D, E lần lượt là hình chiếu của H trên AB, AC. Gọi S là giao điểm của BC, DE. M là trung điểm của BC. Chứng minh SH2 + AM2 = SM2.
Xem lời giải »
Câu 8:
Có bao nhiêu phân số thập phân có tử số là 3, lớn hơn và nhỏ hơn
Xem lời giải »


