Cho tam giác ABC vuông tại A (AB < AC) có AH là đường cao. Gọi D, E lần lượt là hình chiếu của H trên AB, AC. Gọi S là giao điểm của BC, DE. M là trung điểm của BC. Chứng minh SH2 + AM2 = SM2
Câu hỏi:
Cho tam giác ABC vuông tại A (AB < AC) có AH là đường cao. Gọi D, E lần lượt là hình chiếu của H trên AB, AC. Gọi S là giao điểm của BC, DE. M là trung điểm của BC. Chứng minh SH2 + AM2 = SM2.
Trả lời:
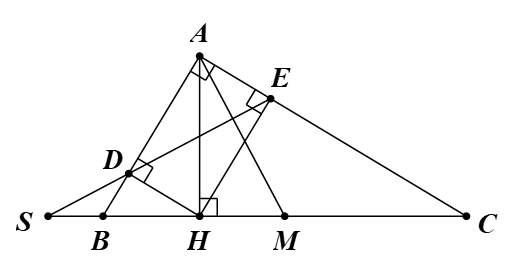
Tam giác ABC vuông tại A có AM là đường trung tuyến.
Suy ra AM = MB = MC.
Tứ giác ADHE, có:
Suy ra tứ giác ADHE là hình chữ nhật.
Xét ∆ADE và ∆EHA, có:
AD = EH (ADHE là hình chữ nhật);
AE chung.
Do đó ∆ADE = ∆EHA (c.g.c).
Suy ra (cặp góc tương ứng).
Mà (đối đỉnh).
Do đó
Vì vậy
Suy ra
Do đó
Xét ∆SHD và ∆SEH, có:
chung;
(chứng minh trên).
Do đó (g.g).
Suy ra
Vì vậy SH2 = SE.SD (1)
Ta có (cùng phụ với ).
Mà (chứng minh trên).
Suy ra
Xét ∆SBD và ∆SEC, có:
chung;
(chứng minh trên).
Do đó (g.g).
Suy ra
Vì vậy SB.SC = SD.SE (2)
Từ (1), (2), suy ra SH2 = SB.SC = (SM – MC)(SM + MC).
= SM2 – MC2 = SM2 – AM2.
Vậy SH2 + AM2 = SM2 (điều phải chứng minh).
