Cho tam giác ABC cân tại A, M là trung điểm của AC, N là trung điểm của AB. BM cắt CN tại K. a) Chứng minh ∆BNC = ∆CMB.

Cho tam giác ABC cân tại A, M là trung điểm của AC, N là trung điểm của AB. BM cắt CN tại K.

a) Chứng minh ∆BNC = ∆CMB.

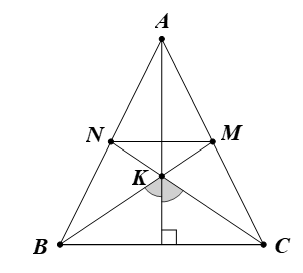
a) Ta có tam giác ABC cân tại A.

Suy ra $\widehat{ABC}=\widehat{ACB}$  và AB = AC.

Ta có M, N lần lượt là trung điểm của AC, AB.

Suy ra $MC=\frac{1}{2}AC$  và $NB=\frac{1}{2}AB$ .

Mà AC = AB (chứng minh trên).

Do đó MC = NB.

Xét ∆BNC và ∆CMB, có:

BC là cạnh chung;

$\widehat{NBC}=\widehat{MCB}$ (chứng minh trên);

MC = NB (chứng minh trên).

Vậy ∆BNC = ∆CMB (c.g.c).