Câu hỏi:
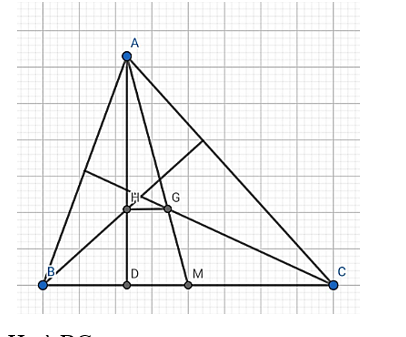
Cho tam giác ABC có 3 góc nhọn, H là trực tâm, G là trọng tâm. Chứng minh rằng nếu tanB. tanC = 3 thì OH // BC.
Trả lời:
Gọi D là giao điểm của AH và BC
⇒ AD ⊥ BC
M là trung điểm BC nên (1)
Xét ΔADC và ΔBDH có:
= 90°
Do đó ΔADC ᔕ ΔBDH(g.g)
⇒
⇒
⇒ tanB. tanC =
⇒ = 3 (2)
Từ (1) và (2) ⇒ =
⇒ HG // BC (định lý Thales đảo).
Câu 2:
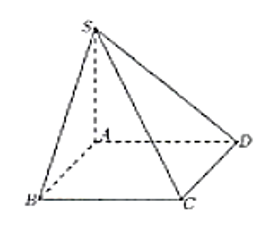
Cho hình chóp S.ABCD có đáy là hình vuông cạnh , SA vuông góc mặt phẳng đáy và SA = (minh họa hình bên). Góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng?
Câu 3:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc mặt phẳng đáy và SB = . Tính thể tích khối chóp S.ABCD?
Câu 4:
Cho tam giác ABC vuông tại A, biết AC = 5 cm, AB = 6 cm và = 45°. Tính các góc , và cạnh BC (sử dụng định lí côsin)?
Câu 5:
Trong một trận đấu gồm 6 đội bóng thi đấu theo thể thức vòng tròn một lượt. Đội thắng được 3 điểm, hoà được 1 điểm, thua 0 điểm. Kết thúc giải đấu, tổng số điểm của cả 6 đội là 41 điểm.
a) Hỏi giải đấu có bao nhiêu trận?
Câu 8:
An và Bình có tất cả 120 viên bi. Nếu An cho Bình 20 viên bi thì Bình sẽ có ít hơn An là 16 viên bi. Vậy mỗi bạn An, Bình có bao nhiêu viên bi?
