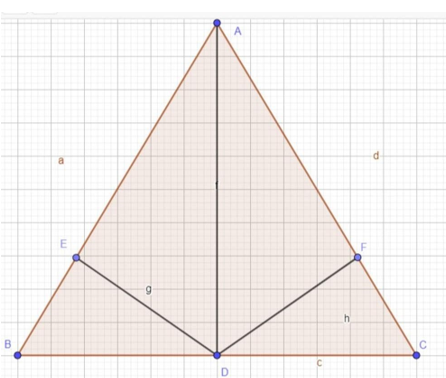
Cho tam giác ABC có AB = AC. Gọi D là trung điểm của BC. Kẻ DE vuông góc với AB; DF vuông góc với AC. Chứng minh a) DEB = DFC
Câu hỏi:
Cho tam giác ABC có AB = AC. Gọi D là trung điểm của BC. Kẻ DE vuông góc với AB; DF vuông góc với AC. Chứng minh
a) DDEB = DDFC
Trả lời:
a) Xét DDEB và DDFC ta có:
(DE ^ AB; DF ^ AC)
BD = DC (vì D là trung điểm của BC)
(vì DABC cân tại A)
Þ DDEB = DDFC (cạnh huyền - góc nhọn)
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Hình chữ nhật có nửa chu vi là 99 m. Nếu tăng chiều rộng thêm 5 m và giảm chiều dài đi 5 m thì diện tích không thay đổi. Tính chiều dài và chiều rộng.
Xem lời giải »
Câu 2:
Tìm số dư của phép chia 158 : 2,8 nếu chỉ lấy đến hai chữ số ở phần thập phân của thương.
Xem lời giải »
Câu 3:
Tìm số tự nhiên a, b biết ƯCLN(a, b) = 4 và a + b = 48.
Xem lời giải »
Câu 4:
Tính diện tích hình thoi có chu vi 52 cm, một đường chéo bằng 24 cm
Xem lời giải »
Câu 6:
Gọi A và B là hai điểm trên Ox sao cho OA = 4 cm, OB = 6 cm. Trên tia BA lấy điểm C sao cho BC = 4 cm.
a) Tính độ dài các đoạn thẳng AB và OC.
Xem lời giải »
Câu 7:
b) Điểm A có phải là trung điểm của đoạn thẳng BC không? Vì sao?
Xem lời giải »
Câu 8:
c) Vẽ tia Cy sao cho và vẽ tia Cz là tia đối của tia Cx, chỉ ra các góc nhọn, góc tù, góc bẹt trong hình?
Xem lời giải »