Cho tam giác ABC có AB = AC. Gọi I là trung điểm của BC, trên tia đối của tia IA lấy
Câu hỏi:
Cho tam giác ABC có AB = AC. Gọi I là trung điểm của BC, trên tia đối của tia IA lấy điểm D sao cho ID = IA.
a) Chứng minh ∆ABI = ∆ACI.
b) Chứng minh AC // BD.
c) Kẻ IK vuông góc với AB (K thuộc AB), IH vuông góc với CD (H thuộc CD). Chứng minh IK = IH.
Trả lời:
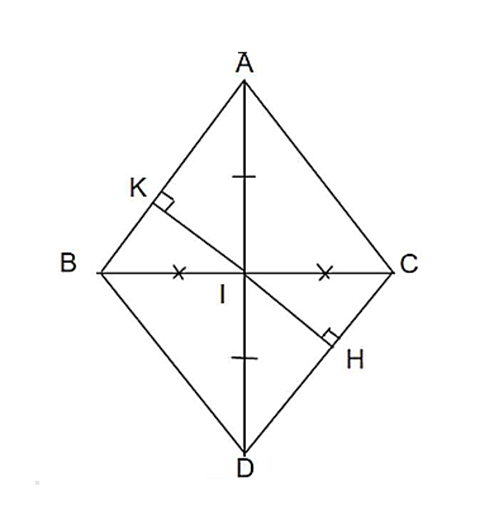
a) Xét ΔABI và ΔACI có:
AB = AC (gt)
BI = CI (I trung điểm BC)
AI chung
⇒ ΔABI = ΔACI (c.c.c).
b)Xét ΔAIC và ΔDIB có:
AI = DI (gt)
\(\widehat {AIC} = \widehat {DIB}\)(đối đỉnh)
IC = IB
⇒ ΔAIC = ΔDIB (c.g.c).
⇒\(\widehat {DIB} = \widehat {ICA}\)(2 góc tương ứng)
Mà chúng so le trong ⇒ AC // BD
c)Xét ΔIKB và ΔIHC có:
\(\widehat {IKB} = \widehat {IHC} = 90^\circ \)
IB = IC
\(\widehat {KIB} = \widehat {CIH}\) (đối đỉnh)
⇒ ΔIKB = ΔIHC (cạnh huyền – góc nhọn)
⇒ IK = IH.

