Cho tam giác ABC có BD, CE là các trung tuyến cắt nhau tại G. a) Tứ giác BEDC hình gì
Câu hỏi:
Cho tam giác ABC có BD, CE là các trung tuyến cắt nhau tại G.
a) Tứ giác BEDC hình gì ?
b) Gọi M, N lần lượt là trung điểm của BG và CG. Chứng minh tứ giác MEDN là hình bình hành.
c) Tam giác ABC có thêm điều kiện gì thì tứ giác MEDN là hình chữ nhật.
Trả lời:
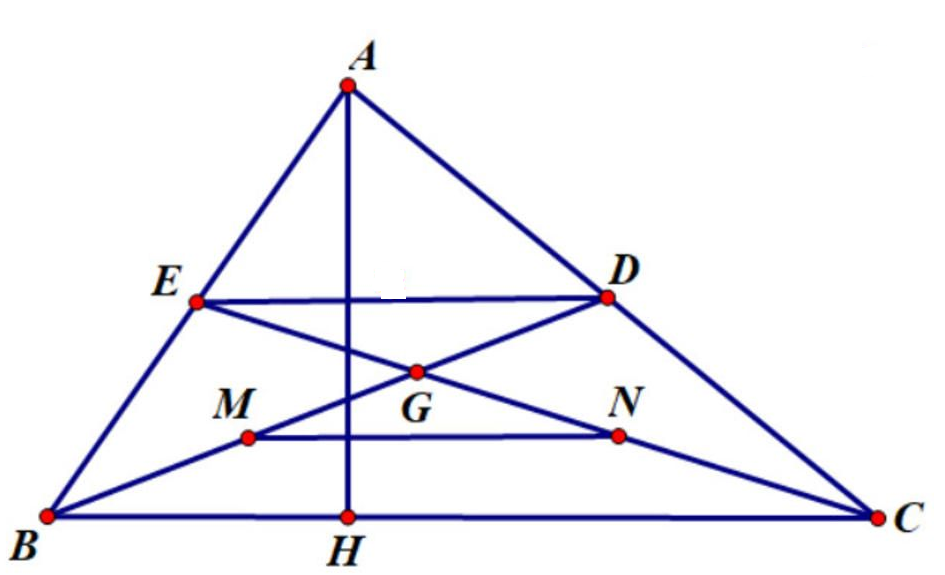
a) Tam giác ABC có E là trung điểm của AB, D là trung điểm của AC
⇒ ED là đường trung bình của tam giác ABC
⇒ ED // BC và ED = BC (1)
⇒ Tứ giác BEDC là hình thang
b) Tam giác GBC có M là trung điểm của GB,N là trung điểm của GC
⇒ MN là đường trung bình của tam giác GBC
⇒ MN // BC và MN = BC (2)
Từ (1), (2) ⇒ ED//MN và ED = MN
⇒ Tứ giác MEDN là hình bình hành
c) Tứ giác MEDN là hình chữ nhật
⇔ MEDN là hình bình hành có 2 đường chéo bằng nhau
⇔ EN = DM
Mà EN = EC, DM = DB
⇒ EC = BD
Hình thang BEDC có EC = BD
⇒ BEDC là hình thang cân ⇒
⇒ Tam giác ABC cân tại A
Vậy tam giác ABC cân tại A thì tứ giác MEDN là hình chữ nhật.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Giải phương trình: (x – 1)(x – 2)(x – 3)(x – 4) = 120.
Xem lời giải »
Câu 2:
Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của BC, CA, AB. Chứng minh rằng: .
Xem lời giải »
Câu 3:
Cho ABC vuông tại A có AB < AC. Gọi D, E lần lượt là trung điểm của các cạnh BC và AC. Trên tia đối của tia DE lấy điểm F sao cho D là trung điểm của cạnh EF.
a) Chứng minh tứ giác BFCE là hình bình hành.
b) Chứng minh tứ giác BFEA là hình chữ nhật.
c) Gọi K là điểm đối xứng với F qua E. Chứng minh tứ giác AFCK là hình thoi.
d) Vẽ AH ⊥ BC tại H. Gọi M là trung điểm của HC. Chứng minh FM ⊥ AM.
Xem lời giải »
Câu 4:
Có 3 bì thư giống nhau lần lượt được đánh số thứ tự từ 1 đến 3 và 3 con tem giống nhau lần lượt đánh số thứ tự từ 1 đến 3. Dán 3 con tem đó vào 3 bì thư sao cho không có bì thư nào không có tem. Tính xác suất để lấy ra được 2 bì thư trong 3 bì thư trên sao cho mỗi bì thư đều có số thứ tự giống với số thứ tự con tem đã dán vào nó
Xem lời giải »
Câu 5:
Xét tất cả các số thực x, y sao cho đúng với mọi số thực dương a. Giá trị lớn nhất của biểu thức P = x2 + y2 + x – 3y bằng:
Xem lời giải »
Câu 6:
Ba ban Lâm, Chí, Dũng có 60 cây bút và số bút tỉ lệ với 3, 4, 5. Tính số bút của mỗi bạn.
Xem lời giải »
Câu 7:
Tìm nghiệm dương nhỏ nhất của phương trình cos2x + 1 = 0.
Xem lời giải »
Câu 8:
Bán kính của một bánh xe ô tô là 0,25m. Tính chu vi bánh xe đó. Nếu ô tô đó đi hết quãng đường dài 4,71km thì bánh xe lăn trên mặt đất được bao nhiêu vòng?
Xem lời giải »


