Cho tam giác ABC có điểm O thỏa mãn |vecto OA + vecto OB - 2 vecto OC| = |ecto OA
Câu hỏi:
Cho tam giác ABC có điểm O thỏa mãn \[\left| {\overrightarrow {OA} + \overrightarrow {OB} - 2\overrightarrow {OC} } \right| = \left| {\overrightarrow {OA} - \overrightarrow {OB} } \right|\]. Hỏi tam giác ABC là tam giác gì?
Trả lời:
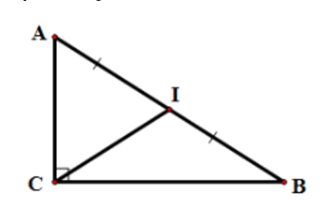
Gọi I là trung điểm AB
Suy ra: \[\overrightarrow {CA} + \overrightarrow {CB} = 2\overrightarrow {CI} \]
Ta có: \[\left| {\overrightarrow {OA} + \overrightarrow {OB} - 2\overrightarrow {OC} } \right| = \left| {\overrightarrow {OA} - \overrightarrow {OB} } \right|\]
⇔ \[\left| {\overrightarrow {OA} - \overrightarrow {OC} + \overrightarrow {OB} - \overrightarrow {OC} } \right| = \left| {\overrightarrow {BA} } \right|\]
⇔ \[\left| {\overrightarrow {CA} + \overrightarrow {CB} } \right| = \left| {\overrightarrow {BA} } \right|\]
⇔ \[\left| {2\overrightarrow {CI} } \right| = AB\]
Hay 2CI = AB
Tức CI = \(\frac{1}{2}AB\)
Do đó tam giác ABC vuông tại C (đường trung tuyến trong tam giác vuông bằng một nửa cạnh huyền).

