Cho tam giác ABC có diện tích là 480cm^2. M là trung điểm của cạnh BC
Câu hỏi:
Cho tam giác ABC có diện tích là 480cm2. M là trung điểm của cạnh BC. N là trung điểm của AM. Nối BN và kéo dài cắt AC tại I.
a) Tính diện tích tam giác BNM.
b) So sánh AI và IC.
Trả lời:
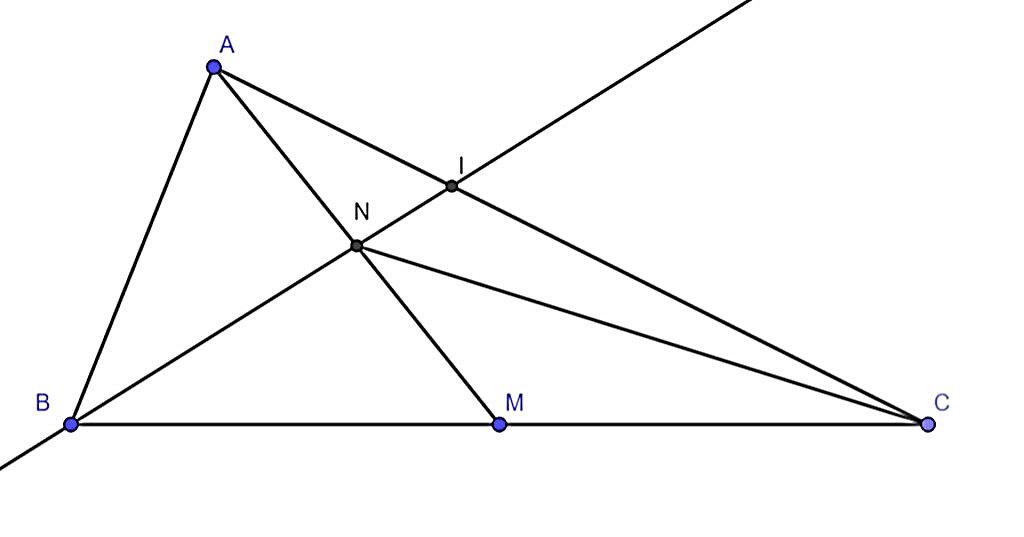
a) SABM = SABC do chung chiều cao từ A, đáy BM = BC
Do đó SABM = 480 : 2 = 240 (cm2)
SBNM = SABM do chung chiều cao từ B, đáy MN = AM
Do đó SBNM = 240 : 2 = 120 (cm2)
b) Nối C với N
SABN = SBNM do chung chiều cao từ B, đáy AN = MN
SMNC = SBNM do chung chiều cao từ C, đáy BM = MC
SCBN = SMNC + SBNM = 2SBNM
Do đó chiều cao từ C xuống đáy NB của ∆CNB bằng hai lần chiều cao từ B xuống NB của ∆ABN.
Đó cũng là chiều cao của ∆AIN và ∆CIN, đáy IN chung nên SCIN = 2SAIN
Hai tam giác này lại có chung chiều cao từ N xuống AC nên đáy AI = IC.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Giải phương trình: (x – 1)(x – 2)(x – 3)(x – 4) = 120.
Xem lời giải »
Câu 2:
Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của BC, CA, AB. Chứng minh rằng: .
Xem lời giải »
Câu 3:
Cho ABC vuông tại A có AB < AC. Gọi D, E lần lượt là trung điểm của các cạnh BC và AC. Trên tia đối của tia DE lấy điểm F sao cho D là trung điểm của cạnh EF.
a) Chứng minh tứ giác BFCE là hình bình hành.
b) Chứng minh tứ giác BFEA là hình chữ nhật.
c) Gọi K là điểm đối xứng với F qua E. Chứng minh tứ giác AFCK là hình thoi.
d) Vẽ AH ⊥ BC tại H. Gọi M là trung điểm của HC. Chứng minh FM ⊥ AM.
Xem lời giải »
Câu 4:
Có 3 bì thư giống nhau lần lượt được đánh số thứ tự từ 1 đến 3 và 3 con tem giống nhau lần lượt đánh số thứ tự từ 1 đến 3. Dán 3 con tem đó vào 3 bì thư sao cho không có bì thư nào không có tem. Tính xác suất để lấy ra được 2 bì thư trong 3 bì thư trên sao cho mỗi bì thư đều có số thứ tự giống với số thứ tự con tem đã dán vào nó
Xem lời giải »
Câu 6:
Cho nửa đường tròn tâm O đường kính AB =2R và điểm M nằm trên đường tròn đó (M ≠ A, B) tiếp tuyến tại điểm M của nửa đường tròn tâm O cắt các tiếp tuyến tại A và B. Lần lượt tại các điểm C, D. Gọi E là giao điểm của OC với AM, gọi F là giao điểm của OD và BM.
a) Chứng minh CD = AC + BD.
b) Chứng minh EF vuông góc BD và EF là tiếp tuyến đường tròn đi qua các điểm M, D, F.
Xem lời giải »
Câu 7:
Cho đường tròn tâm O, điểm M bất kỳ bên ngoài đường tròn. Vẽ các tiếp tuyến MA và MB với đường tròn. Vẽ đường kính AC. Chứng minh 4 điểm A, B, C, O cùng nằm trên 1 tam giác vuông.
Xem lời giải »
Câu 8:
Chứng minh giá trị của biểu thức sau không phụ thuộc vào biến x.
A = x(3x2 – x + 5) – (2x3 + 3x – 25) – x(x2 – x + 2).
B = x(2x + 1) – x2(x + 2) + (x3 – x + 10).
Xem lời giải »


