Cho tam giác ABC đều có cạnh 3 cm. a) Tính diện tích tam giác ABC.
Câu hỏi:
Cho tam giác ABC đều có cạnh 3 cm.
a) Tính diện tích tam giác ABC.
b) Lấy M nằm trong tam giác ABC. Vẽ MI, MJ, MK lần lượt vuông góc với AB, AC, BC. Hãy tính MI + MJ + MK.
Trả lời:
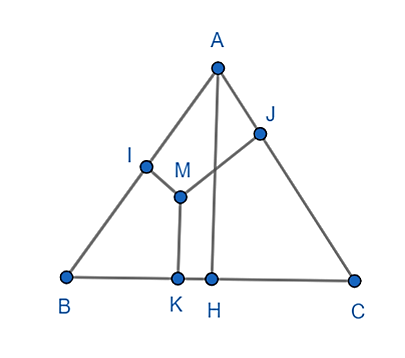
Kẻ AH vuông góc với BC (H thuộc BC)
Vì ABC là tam giác đều nên AH là đường cao đồng thời là đường trung tuyến. Suy ra H là trung điểm BC
Áp dụng định lý Pytago trong tam giác AHC có:
AH2 = AC2 – HC2 = 32 –
Suy ra: AH =
SABC = (cm2)
b) SAMB =
SAMC =
SCMB =
SABC = SAMB + SAMC + SBMC = 1,5 (MI + MJ + MK) =
MI + MJ + MK = (cm).

