Câu hỏi:
Cho tam giác ABC, . Kẻ đường cao AH. Trên tia đối của tia HA lấy điểm K sao cho HK = HA. Chứng minh ΔABH = ΔKBH.
Trả lời:
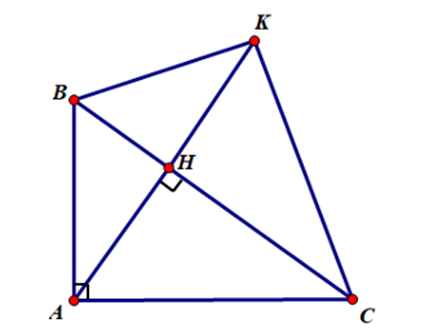
Xét ΔABH và ΔKBH có:
AH = KH (gt)
BH cạnh chung
Do đó ΔABH = ΔKBH (c.g.c)
Câu 3:
Cho tam giác ABC vuông tại A. Đường cao AH. Kẻ phân giác của cắt AH tại M, kẻ phân giác của cắt BH tại N. Chứng minh rằng MN // AB.
Câu 5:
Cho các hàm số: y = 2x − 2 và y = (m + 1)x −𝑚2 – 𝑚 (m ≠ −1). Tìm m để đồ thị hai hàm số trên là các đường thẳng song song.
Câu 6:
Tìm m để hai đường thẳng (d): y = 3x + 1 và (d′): y = (m−1)x − 2m song song với nhau.
Câu 7:
Cổng Arch tại thành phố St Louis của Mỹ có hình dạng là một parabol (hình vẽ). Biết khoảng cách giữa hai chân cổng bằng 162 m. Trên thành cổng, tại vị trí có độ cao 43 m so với mặt đất (điểm M), người ta thả một sợi dây chạm đất (dây căng thẳng theo phương vuông góc với đất). Vị trí chạm đất của đầu sợi dây này cách chân cổng A một đoạn 10 m. Giả sử các số liệu trên là chính xác. Hãy tính độ cao của cổng Arch (tính từ mặt đất đến điểm cao nhất của cổng).
