Cho tam giác ABC nhọn có trực tâm H. Chứng minh tan A . vecto HA + tan B . vecto HB
Câu hỏi:
Cho tam giác ABC nhọn có trực tâm H. Chứng minh:
\(\tan A.\overrightarrow {HA} + \tan B.\overrightarrow {HB} + \tan C.\overrightarrow {HC} = \overrightarrow 0 \).
Trả lời:
Cần chứng minh: \(\tan A.\overrightarrow {HA} + \tan B.\overrightarrow {HB} + \tan C.\overrightarrow {HC} = \overrightarrow 0 \)
⇔ \[\overrightarrow {HC} = - \frac{{\tan A}}{{\tan C}}.\overrightarrow {HA} - \frac{{\tan B}}{{\tan C}}.\overrightarrow {HB} \]
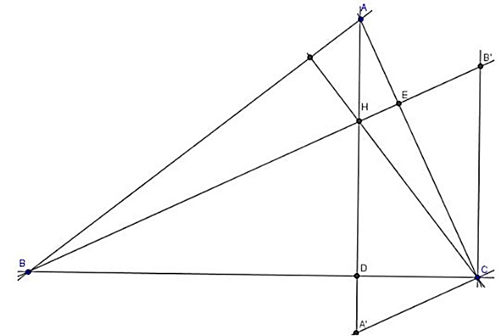
Vẽ hình bình hành HB’CA’ ta có:
\(\left\{ \begin{array}{l}\frac{{HB'}}{{HB}} = \frac{{DC}}{{DB}}\\\frac{{\tan B}}{{\tan C}} = \frac{{AD}}{{BD}}:\frac{{AD}}{{DC}} = \frac{{DC}}{{DB}}\end{array} \right.\)
Suy ra: \(\frac{{HB'}}{{HB}} = \frac{{\tan B}}{{\tan C}}\)
⇒ \[\overrightarrow {HB'} = - \frac{{\tan B}}{{\tan C}}.\overrightarrow {HB} \](do \[\overrightarrow {HB'} ;\overrightarrow {HB} \]ngược hướng)
Tương tự: \[\overrightarrow {HA'} = - \frac{{\tan A}}{{\tan C}}.\overrightarrow {HA} \]
⇒ \[\overrightarrow {HB'} + \overrightarrow {HA'} = - \frac{{\tan B}}{{\tan C}}.\overrightarrow {HB} - \frac{{\tan A}}{{\tan C}}.\overrightarrow {HA} \]
Mà: \[\overrightarrow {HB'} + \overrightarrow {HA'} = \overrightarrow {HC} \]
Nên: \[\overrightarrow {HC} = - \frac{{\tan A}}{{\tan C}}.\overrightarrow {HA} - \frac{{\tan B}}{{\tan C}}.\overrightarrow {HB} \]
Vậy \(\tan A.\overrightarrow {HA} + \tan B.\overrightarrow {HB} + \tan C.\overrightarrow {HC} = \overrightarrow 0 \).

