Cho tam giác ABC nhọn. Gọi M và N lần lượt là trung điểm của AB, BC. a) Tính độ dài của MN biết AC = 16cm. b) Gọi I là trung điểm của AC. Chứng minh tứ giác BMIN là hình bình hành. c) Trên
Câu hỏi:
Cho tam giác ABC nhọn. Gọi M và N lần lượt là trung điểm của AB, BC.
a) Tính độ dài của MN biết AC = 16cm.
b) Gọi I là trung điểm của AC. Chứng minh tứ giác BMIN là hình bình hành.
c) Trên tia đối của tia NM lấy E sao cho N là trung điểm ME. Gọi K là giao điểm của EI và MC. Chứng minh MC = 3KC.
Trả lời:
Lời giải
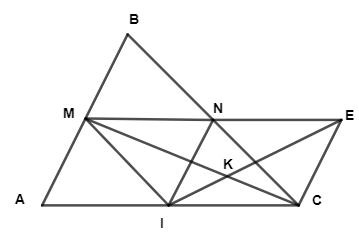
a) Xét ΔABC có: M là trung điểm của AB, N là trung điểm của BC
Do đó: MN là đường trung bình của ∆ABC
Suy ra: MN // AC và \(MN = \frac{{AC}}{2} = \frac{{16}}{2} = 8\) (cm)
b) Xét ∆ABC có M là trung điểm của AB, I là trung điểm của AC
Do đó: MI là đường trung bình của ∆ABC
Suy ra: MI // BC và \(MI = \frac{{BC}}{2}\)
Mà \(BN = \frac{{BC}}{2}\) nên MI // BN và MI = BN
Do đó tứ giác BMIN là hình bình hành
c) Ta có: \(MN = NE = \frac{{AC}}{2} = IC\)
Mà MN // IC nên NE // IC
Do đó tứ giác NECI là hình bình hành
Mà K là giao điểm của EI và MC nên \(\frac{{KC}}{{KM}} = \frac{{IC}}{{ME}} \Rightarrow \frac{{KC}}{{KM}} = \frac{1}{2}\) ⇒ KM = 2KC
Ta có: KM + KC = MC ⇔ 2KC + KC = MC ⇔ 3KC = MC
Vậy 3KC = MC
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Tìm x, biết: \({x^2} + 5x + 4 - 5\sqrt {{x^2} + 5x + 28} = 0\).
Xem lời giải »
Câu 2:
Cho định lí “Cho số tự nhiên n, nếu n5 chia hết cho 5 thì n chia hết cho 5”.
Định lí này được viết dưới dạng P Þ Q. Hãy phát biểu định lí đảo của định lí trên rồi dùng các thuật ngữ “điều kiện cần và đủ” phát biểu gộp cả 2 định lí thuận và đảo.
Xem lời giải »
Câu 3:
Viết các số (0,25)8 và (0,125)4 dưới dạng các lũy thừa với cơ số 0,5.
Xem lời giải »
Câu 4:
Cho một hộp đựng 4 viên bi đỏ, 5 viên bi xanh và 7 viên bi vàng. Lấy ngẫu nhiên một lần ba viên bi. Tính xác suất để trong ba viên bi lấy được chỉ có hai màu.
Xem lời giải »
Câu 5:
Cho tam giác ABC vuông cân tại A. Ở phía ngoài tam giác ABC, vẽ tam giác BCD vuông cân tại B. Tứ giác ABCD là hình gì? Vì sao?
Xem lời giải »
Câu 6:
Cho tam giác ABC vuông tại A, đường cao AH, M là trung điểm của BC, có BH = 4 cm, CH = 9 cm. Tính diện tích tam giác AHM?
Xem lời giải »
Câu 7:
Cho đường tròn (O), đường kính AB cố định, M là 1 điểm thuộc (O), (M khác A và B). Các tiếp tuyến của (O) tại A và M cắt nhau ở C. Đường tròn (I) đi qua M và tiếp xúc với đường thẳng AC tại C, CD là đường kính của (I). Chứng minh rằng:
a) 3 điểm O, M, D thẳng hàng.
b) Tam giác COD là tam giác cân.
c) Gọi N là giao điểm của OC và (I). Chứng minh khi M thay đổi thì đường thẳng qua N vuông góc với AB luôn đi qua điểm cố định.
Xem lời giải »
Câu 8:
Cho đường tròn (O), đường kính BC = 2R, điểm A nằm ngoài đường tròn sao cho tam giác ABC nhọn. Từ A kẻ 2 tiếp tuyến AM, AN với đường tròn (O). Gọi H là trực tâm của tam giác ABC, F là giao điểm của AH và BC. Chứng minh rằng:
a, 5 điểm A, O, M, N, F cùng nằm trên 1 đường tròn.
b, 3 điểm M, N, H thẳng hàng.
c, HA . HF = R2 – OH2.
Xem lời giải »


