Cho tam giác ABC. Về phía ngoài vẽ 3 tam giác đều ABC', BCA', CAB'. Chứng minh AA', BB', CC' bằng nhau và đồng quy.
Câu hỏi:
Cho tam giác ABC. Về phía ngoài vẽ 3 tam giác đều ABC', BCA', CAB'. Chứng minh AA', BB', CC' bằng nhau và đồng quy.
Trả lời:
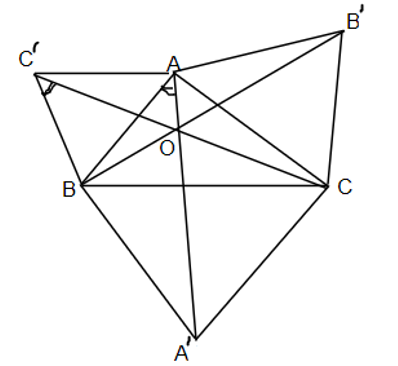
Gọi O là giao điểm của AA' và CC'. Ta chứng minh .
Ta có: vì C'B = AB, BC = BA', .
Do đó, ΔC'BC = ΔABA' (cgc).
Suy ra .
Do đó, C'BOA là tứ giác nội tiếp đường tròn.
và (cùng chắn hai cung có độ dài bằng nhau).
Tương tự ta có các góc AOB', B'OC, COA', A'OB đều bằng 60°.
Suy ra
Vậy BOB' thẳng hàng.
Vậy AA', BB', CC' đồng quy tại O.
Từ ΔC'BC = ΔABA' suy ra CC' = AA'. Chứng minh tương tự suy ra AA' = BB'.
Vậy AA' = BB' = CC'.

