Cho tam giác ABC vuông cân tại A, M là trung điểm của AC, trên BM lấy điểm N sao cho
Câu hỏi:
Cho tam giác ABC vuông cân tại A, M là trung điểm của AC, trên BM lấy điểm N sao cho NM = MA ; CN cắt AB tại E. Chứng minh:
a) Tam giác BNE đồng dạng với tam giác BAN.
b) \(\frac{{NC}}{{AN}} = \frac{{NB}}{{AB}} + 1\).
Trả lời:
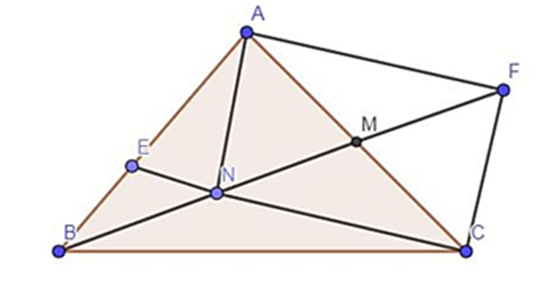
a) ΔANC vuông tại N ( trung tuyến bằng nữa cạnh đối diện)
Nên \(\widehat {CNM} + \widehat {MNA} = 90^\circ \)
\(\widehat {BAN} + \widehat {NAC} = 90^\circ \)
\(\widehat {NAC} = \widehat {MNA}\)
⇒ \(\widehat {CNM} = \widehat {BAN}\)
Mà \(\widehat {CNM} = \widehat {BNE}\)
⇒ \[\widehat {BAN} = \widehat {BNE}\]
Vậy ΔBNE ∽ ΔBAN.
b) Trên tia đối MN lấy điểm F sao cho FM = MN
Khi đó tứ giác ANCF là hình chữ nhật
⇒ CE // AF, FN = AC
⇒ \(\widehat {AFB} = \widehat {ENB} = \widehat {BAC}\)
Xét ΔBAN và ΔBFA có:
Chung \(\widehat B\)
\(\widehat {BAN} = \widehat {AFB}\)(= \(\widehat {ENB}\))
⇒ ΔBAN ∽ ΔBFA
⇒ \(\frac{{FA}}{{AN}} = \frac{{BF}}{{BA}}\)
⇒ \(\frac{{NC}}{{AN}} = \frac{{FN + NB}}{{AB}} = \frac{{AB + NB}}{{AB}} = \frac{{NB}}{{AB}} + 1\) (vì FN = AC = AB).

