Cho tam giác ABC vuông cân tại A. Trên các cạnh AB, AC lấy tương ứng hai điểm D, E sao cho AD = AE. Từ A và D kẻ đường vuông góc với BE và cắt BC tại M, N. Tia ND cắt tia CA ở I. Chứng minh A
Câu hỏi:
Cho tam giác ABC vuông cân tại A. Trên các cạnh AB, AC lấy tương ứng hai điểm D, E sao cho AD = AE. Từ A và D kẻ đường vuông góc với BE và cắt BC tại M, N. Tia ND cắt tia CA ở I. Chứng minh A là trung điểm của CI.
Trả lời:
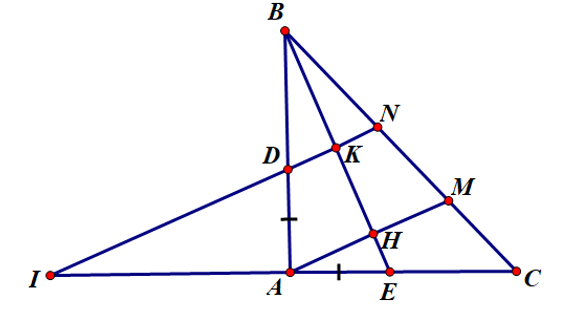
Gọi K là giao điểm của DN và BE
• Xét ΔBDK vuông tại K có:
• Xét ΔABE vuông tại A có:
Suy ra
Mà (vì hai góc đối đỉnh)
Suy ra
• Xét ΔDAI và ΔEAB có:
AD = AE
Do đó ΔDAI = ΔEAB (cạnh góc vuông – góc nhọn)
Suy ra AI = AB (hai cạnh tương ứng).
Mà AB = AC nên AI = AC.
Vậy A là trung điểm của CI.

