Cho tam giác ABC vuông tại A , AB = AC. Qua A vẽ đường thẳng d sao cho B và C
Câu hỏi:
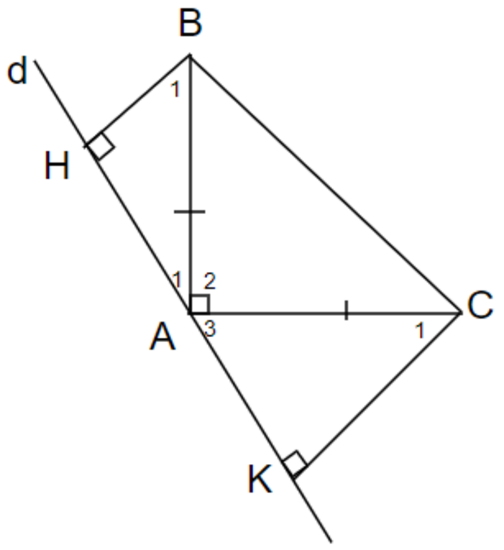
Cho tam giác ABC vuông tại A , AB = AC. Qua A vẽ đường thẳng d sao cho B và C nằm cùng phía đối với đường thẳng d . Kẻ BH và CK vuông góc với d.
Chứng minh:
a) AH = CK.
b) HK = BH + CK.
Trả lời:
a) Ta có: = 180° (Vì là góc bẹt)
=> = 90° (Vì = 90°) (1)
Xét ΔAKC có: = 90° (Vì = 90°) (2)
Từ (1) và (2) suy ra: .
Xét ΔAHB và ΔCKA có:
(cmt)
AB = AC (gt)
= 90°
Do đó: ΔAHB = ΔCKA (cạnh huyền - góc nhọn)
⇒ AH = CK (Cặp cạnh tương ứng)
b) Vì ΔAHB = ΔCKA nên BH = AK và AH = CK (Cặp cạnh tương ứng)
Ta có: HK = AK + AH = BH + CK (đpcm)
Vậy HK = BH + CK.

