Cho tam giác ABC vuông tại A có đường cao AH biết AC = 20 cm, BH = 9 cm. Tính BC và AH?

Câu hỏi:

Trả lời:

Lời giải

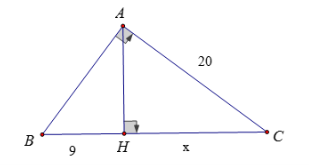
Đặt HC = x (cm)

Xét tam giác ABC vuông tại A có AH ⊥ BC

Theo hệ thức lượng trong tam giác vuông, ta có:

AC² = CH . BC

\( \Rightarrow {20^2} = \left( {9 + x} \right)x\)

\( \Leftrightarrow {x^2} + 9x - 400 = 0\)

\( \Leftrightarrow \left( {x + 25} \right)\left( {x - 16} \right) = 0\)

\[ \Leftrightarrow \left[ \begin{array}{l}x = - 25\left( {ktm} \right)\\x = 16\end{array} \right.\]

Suy ra BC = BH + CH = 9 + 16 = 25 (cm)

Xét tam giác ABC vuông tại A có AH ⊥ BC

Theo hệ thức lượng trong tam giác vuông, ta có:

AH² = CH . BH = 9 . 16 = 144

Suy ra AH = 12 (cm)

Vậy BC = 25 cm, AH = 12 cm.