Cho tam giác nhọn ABC. Các đường cao AD và BE cắt nhau tại H. Đường thẳng vuông góc với AB tại A cắt BE ở K. Chứng minh tam giác EAK đồng dạng tam giác ECH.

Cho tam giác nhọn ABC. Các đường cao AD và BE cắt nhau tại H. Đường thẳng vuông góc với AB tại A cắt BE ở K. Chứng minh tam giác EAK đồng dạng tam giác ECH.

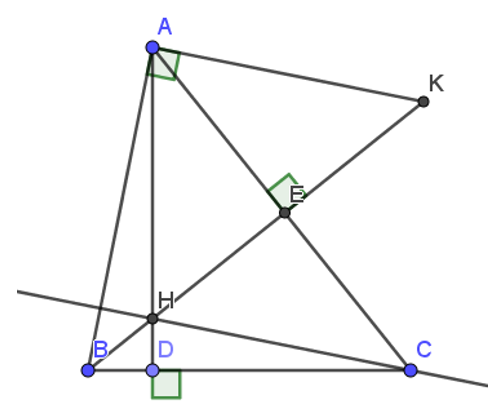
Vì H là giao của 2 đường cao AD, BE trong tam giác nên H là trực tâm.

Do đó, CH cũng là đường cao của tam giác ABC hay CH vuông góc với AB

Mà AK vuông góc với AB (giả thiết)

Suy ra: CH song song với AK

$\Rightarrow \widehat{HCE}=\widehat{KAE}$ (so le trong)

Xét tam giác EAK và ECH có:

$\widehat{HCE}=\widehat{KAE}$

$\widehat{AEK}=\widehat{CEH}=90°$

Do đó, tam giác EAK đồng dạng với tam giác ECH (g.g).